|
|
Diffusion (lateinisch diffusio, von lateinisch diffundere „ausgießen“, „verstreuen“, „ausbreiten“) ist der ohne äußere Einwirkung eintretende Ausgleich von Konzentrationsunterschieden in Flüssigkeiten oder Gasen als natürlich ablaufender physikalischer Prozess aufgrund der brownschen Molekularbewegung. Er führt mit der Zeit zur vollständigen Durchmischung zweier oder mehrerer Stoffe durch die gleichmäßige Verteilung der beweglichen Teilchen[1] und erhöht damit die Entropie des Systems. Bei den Teilchen kann es sich um Atome, Moleküle, Ladungsträger oder auch um freie Neutronen[2] handeln. Meist ist zumindest einer der Stoffe ein Gas oder eine Flüssigkeit, doch können auch Feststoffe und Plasmen ineinander diffundieren.
Funktionsprinzip
Diffusion beruht auf der ungerichteten Zufallsbewegung von Teilchen aufgrund ihrer thermischen Energie („thermische Bewegung“, s. u.). Bei ungleichmäßiger Verteilung bewegen sich statistisch mehr Teilchen aus Bereichen hoher in Bereiche geringer Konzentration bzw. Teilchendichte, als umgekehrt. Dadurch wird netto ein makroskopischer Stofftransport bewirkt. Unter Diffusion versteht man in der Regel diesen Netto-Transport. Der Begriff wird aber auch für den zugrundeliegenden mikroskopischen Prozess verwendet.
In einem abgeschlossenen System bewirkt Diffusion den Abbau von Konzentrationsunterschieden bis hin zur vollständigen Durchmischung. Die Zeit, die dafür benötigt wird, wächst im n {displaystyle n} -dimensionalen Raum mit der n {displaystyle n} -ten Potenz des Abstands. Diffusion ist daher vor allem auf Nano- bis Millimeter-Skalen wirksam; auf größeren Skalen dominiert in Flüssigkeiten und Gasen in der Regel Stofftransport durch Strömung (Konvektion). Die Diffusion in Feststoffen wird zudem häufig durch andere chemisch-physikalische Vorgänge wie Absorption, Adsorption, Resorption und Kapillartransport überlagert.
Diffusion ist nicht von der Luftdurchlässigkeit eines Materials abhängig. Bei der Osmose diffundieren kleine Moleküle durch eine geschlossene Membran, die für größere Moleküle undurchlässig ist. Entscheidend ist die Diffusivität des Materials in Bezug auf den diffundierenden Stoff.
Diffusion kann auf verschiedenen Phänomenen beruhen:
- Kollektive Diffusion ist die Diffusion mehrerer Teilchen entlang eines Konzentrationsgradienten, darunter fallen beispielsweise die Fickschen Gesetze.
- Bei der Selbstdiffusion werden dagegen einzelne Teilchen betrachtet, deren Verhalten u. a. von der Einsteinrelation beschrieben wird. Der Selbstdiffusionskoeffizient D S ( t ) {displaystyle D_{text{S}}(t)} (Subskript S steht für Selbstdiffusion) ist eine Funktion der Zeit.
- Für extrem kurze Zeiten kleiner der Brownschen Relaxationszeit spricht man vom ballistischen Regime.
- Für Zeiten in der Nähe der Brownschen Relaxationszeit τ 0 {displaystyle tau _{0}} herrscht die Kurzzeitdiffusionskonstante D S k = lim t → τ 0 D S ( t ) {displaystyle D_{text{S}}^{text{k}}=lim _{tto tau _{0}}D_{text{S}}(t)} vor.
- Demgegenüber dominiert im Limes großer Zeiten die Langzeitdiffusionskonstante D S l = lim t → ∞ D S ( t ) {displaystyle D_{text{S}}^{text{l}}=lim _{tto infty }D_{text{S}}(t)} .
Geschichte
Einer der Ersten, die systematisch Diffusionsversuche in größerem Umfang durchführten, war Thomas Graham. Aus seinen Experimenten zur Diffusion von Gasen leitete er das nach ihm benannte Grahamsche Gesetz ab:
“It is evident that the diffusiveness of the gases is inversely as some function of their density – apparently the square root of their density.”
„Es ist offensichtlich, dass die Diffusionsrate der Gase invers zu einer Funktion ihrer Dichte ist – anscheinend zur Quadratwurzel ihrer Dichte.“[3]
“The diffusion or spontaneous intermixture of two gases in contact, is effected by an interchange in position of indefinitely minute volumes of the gases, which volumes are not necessarily of equal magnitude, being, in the case of each gas, inversely proportional to the square root of the density of that gas.”
„Die Diffusion oder spontane Mischung von zwei sich in Kontakt befindenden Gasen wird beeinflusst durch den Austausch der Position von unbestimmt kleinen Volumina der Gase, die nicht unbedingt von gleicher Größenordnung sein müssen und, im Fall jedes Gases, invers proportional zur Quadratwurzel der Dichte des Gases sind.“[4]
In Hinblick auf Diffusion in Lösungen konnte Graham zeigen, dass die Diffusionsrate proportional zu Konzentrationsdifferenz und abhängig von der Temperatur ist (schnellere Diffusion bei höheren Temperaturen).[5] Weiterhin zeigte Graham die Möglichkeit auf, Mischungen von Lösungen oder Gasen mittels Diffusion zu trennen.[3][5]
Thomas Graham hatte die grundlegenden Gesetze der Diffusion noch nicht ermitteln können. Dies gelang nur wenige Jahre später Adolf Fick. Er postulierte, dass das gesuchte Gesetz analog zu den Gesetzmäßigkeiten der Wärmeleitung, die Jean Baptiste Joseph Fourier ermittelt hatte, sein müsse:
„Die Verbreitung eines gelösten Körpers im Lösungsmittel geht, wofern sie ungestört unter dem ausschließlichen Einfluß der Molekularkräfte stattfindet, nach demselben Gesetze vor sich, welches Fourier für die Verbreitung der Wärme in einem Leiter aufgestellt hat, und welches Ohm bereits mit so glänzendem Erfolge auf die Verbreiterung der Elektrizität (wo es freilich bekanntlich nicht streng richtig ist) übertragen hat.“[6]
Fick führte Experimente durch, deren Ergebnisse die Gültigkeit des später nach ihm benannten Ersten Fickschen Gesetzes belegten. Die Gültigkeit des Zweiten Fickschen Gesetzes konnte er nur aus der Gültigkeit des Ersten herleiten. Der direkte Nachweis scheiterte an seinen begrenzten analytischen und mathematischen Möglichkeiten.
Albert Einstein gelang es Anfang des 20. Jahrhunderts, die Fickschen Gesetze aus den Gesetzen der Thermodynamik abzuleiten und so der Diffusion ein sicheres theoretisches Fundament zu geben.[7] Dabei leitete er auch die Stokes-Einstein-Beziehung zur Berechnung des Diffusionskoeffizienten her:
„Der Diffusionskoeffizient der suspendierten Substanz hängt also außer von universellen Konstanten und der absoluten Temperatur nur vom Reibungskoeffizienten der Flüssigkeit und von der Größe der suspendierten Teilchen ab.“
Einstein zeigte auch, wie man die Bewegung eines einzelnen diffundierenden Teilchens erfassen kann und damit die Brown’sche Molekularbewegung als ein Fluktuationsphänomen verstehen kann. Er berechnete die mittlere quadratische Verschiebung ⟨ r 2 ( τ ) ⟩ {displaystyle langle r^{2}(tau )rangle } eines Teilchens in der Zeit τ für den eindimensionalen Fall zu ⟨ r 2 ( τ ) ⟩ = 2 D τ {displaystyle langle r^{2}(tau )rangle =2Dtau } . Kurze Zeit nach Einstein kam Smoluchowski auf einem anderen Weg ebenfalls zu praktisch derselben Beziehung, und daher wird diese Gleichung heute als Einstein-Smoluchowski-Gleichung bezeichnet.
Veranschaulichung
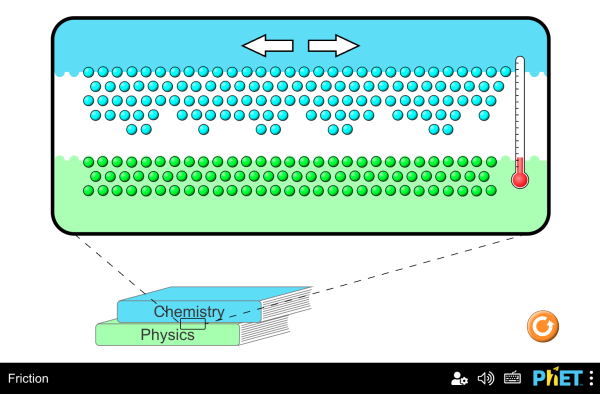
Ein oft genanntes Experiment zur Veranschaulichung der Ausbreitung durch Diffusion ist die allmähliche Einfärbung von lauwarmem Wasser durch einen Tropfen Tinte, den man hineingibt, das Wasser aber weder umrührt noch den Behälter schüttelt. Nach einiger Zeit hat sich die Tintenfarbe im ganzen Wasser gleichmäßig verteilt. Die Ausbreitung der Tinte im Wasser kann allerdings auch durch Dichte– und Temperaturunterschiede begünstigt werden. Diese Einflüsse lassen sich verringern, indem man eine farbige Flüssigkeit mit höherer Dichte mit einer Flüssigkeit mit niedrigerer Dichte überschichtet und sehr viskose Flüssigkeiten verwendet, z. B. farbigen Sirup und Honig. Die dann beobachtete allmähliche Einfärbung des Honigs erklärt sich nahezu ausschließlich durch Diffusion, wobei sowohl Sirup in den Honig als auch Honig in den Sirup diffundiert.
Praktische Beispiele
- Beim Sintern spielt die Diffusion eine sehr wichtige Rolle beim Zusammenwachsen der Pulverbestandteile.
- Stahl kann durch Eindiffundieren von Kohlenstoff und/oder Stickstoff randschichtgehärtet werden oder zu Metal Dusting führen.
- In Diffusionsöfen werden bei Temperaturen um 1000 °C Dotanden in das Halbleitermaterial eingebracht, um dort gezielt die elektrische Leitfähigkeit oder mechanische Eigenschaften für Bauelemente der Mikrosystemtechnik zu beeinflussen.
- Die Diffusion spielt in der Technischen Chemie eine zentrale Rolle. Häufig tritt sie hier gekoppelt mit Konvektion und chemischen Reaktionen auf. Typische Anwendungen sind Reaktor- und Katalysatordesign. In der chemischen Verfahrenstechnik erfolgt die selektive Trennung von Stoffgemischen häufig mittels Molekularsieb– und/oder Membrantechnik. Beide Verfahren beruhen auf „kinetischer Separation“, wobei die Differenzen der Diffusion der einzelnen Stoffe in Nanoporen eine wesentliche Rolle spielen und sich dadurch Steuerungsmöglichkeiten eröffnen.
- In Halbleitern bewegen sich Elektronen aufgrund eines Diffusionsstromes entgegen dem durch die Spannungsquelle erzeugten Feldstrom.
- Bei ambipolarer Diffusion bewegen sich Elektronen und Ionen gleichgerichtet im Plasma.
- Bei der Baukonstruktion muss zum Feuchteschutz die Wasserdampfdiffusion berücksichtigt werden, um unzulässig große Tauwasserkondensation zu vermeiden. Dazu werden Dampfsperren und Dampfbremsen mit definiertem Wasserdampfdiffusionswiderstand eingesetzt.
- In der Mikrobiologie wird Diffusion beim Agardiffusionstest genutzt.
- Bei der Lungenatmung erfolgt der Gasaustausch zwischen Lungenbläschen und Blut durch Diffusion.
- Mit der sogenannten diffusion-ordered-spectroscopy (DOSY) kann in Mischungen die translatorische Beweglichkeit einzelner Moleküle gemessen und anhand des Diffusionskoeffizienten das Molekülgewicht bestimmt werden.[8]
Physikalische Grundlagen
Die Diffusion bei einer bestimmten konstanten Temperatur erfolgt ohne weitere Energiezufuhr und ist in diesem Sinne passiv; vor allem in der Biologie wird die Diffusion vom aktiven Transport unterschieden.
Theoretisch ist Diffusion ein unendlich lange dauernder Vorgang. Im Rahmen der Messbarkeit kann sie jedoch häufig als in endlicher Zeit abgeschlossen betrachtet werden.
Thermische Bewegung
Die thermische Bewegung, auf der die Diffusion beruht, kann je nach betrachtetem System einen sehr unterschiedlichen Charakter haben. In Gasen ist sie geradlinig. unterbrochen von gelegentlichen Stößen. Die schnelle thermische Bewegung von Flüssigkeitsteilchen bewirkt durch häufige Stöße die wesentlich langsamere, unter dem Mikroskop beobachtbare Brownsche Bewegung mesoskopischer Objekte. In Festkörpern erfolgen gelegentliche Ortswechsel, z. B. durch den Platztausch zweier benachbarter Teilchen, oder das „Wandern“ von Leerstellen. Bei Ladungsträgern (z. B. Ionen, Elektronen, Löchern) ist der Wärmebewegung jedoch ein Drift durch die elektrostatischen Kräfte überlagert.
Wahrscheinlichkeit und Entropie
Die Bewegungsrichtung eines einzelnen Teilchens ist vollkommen zufällig. Aufgrund der Wechselwirkung mit anderen Teilchen erfolgen ständige Richtungsänderungen. Über einen längeren Zeitraum bzw. über viele Teilchen gemittelt kann sich dennoch ein Transport in eine bestimmte Richtung ergeben, z. B. wenn ein Sprung in eine bestimmte Richtung eine, vielleicht nur geringfügig, größere Wahrscheinlichkeit hat. Dies ist der Fall, wenn ein Konzentrationsunterschied (auch Konzentrationsgradient) vorhanden ist. Es entsteht dann ein Nettofluss an Teilchen, bis sich ein stationärer Zustand, das thermodynamische Gleichgewicht, einstellt. Zumeist ist der Gleichgewichtszustand die Gleichverteilung, bei der die Konzentration aller Teilchen an jedem Punkt im Raum gleich hoch ist.
Wahrscheinlichkeit und Diffusion – ein Erklärungsversuch: Angenommen 1000 Teilchen eines Stoffes wären nur in der rechten Hälfte eines Gefäßes, und 10 Teilchen in der linken Hälfte; außerdem bewegt sich jedes Teilchen durch die Brownsche Molekularbewegung eine bestimmte Strecke in eine völlig zufällige Richtung. Dann folgt: Die Wahrscheinlichkeit, dass sich eines der 1000 Teilchen zufälligerweise von der rechten in die linke Hälfte bewegt ist 100-mal größer als die Wahrscheinlichkeit, dass sich eines der nur 10 Teilchen von links nach rechts bewegt. Also werden nach einer gewissen Zeit mit hoher Wahrscheinlichkeit netto Teilchen von rechts nach links gewandert sein. Sobald die Wahrscheinlichkeit des Wanderns auf beiden Seiten gleich groß ist, sich also rechts und links je 505 Teilchen befinden, wird netto kein Massenfluss mehr stattfinden und die Konzentration bleibt überall (im Rahmen statistischer Schwankungen) gleich groß. Selbstverständlich wandern nach wie vor Teilchen von links nach rechts und umgekehrt; da es aber nun gleich viele Teile sind, lässt sich kein Unterschied in der Konzentration feststellen. Wenn man sich jetzt „rechts“ und „links“ als besonders kleine Teilräume z. B. des Tintenversuches vorstellt und alle diese Teilräume irgendwann alle die gleiche Tintenkonzentration aufweisen, hat sich die Tinte gleichmäßig verteilt.
Systeme, in denen die Teilchen regellos über das ganze Volumen verteilt sind, haben eine höhere Entropie als geordnetere Systeme, in denen sich die Teilchen bevorzugt in bestimmten Bereichen aufhalten. Diffusion führt damit zu einer Entropieerhöhung. Sie ist nach dem Zweiten Hauptsatz der Thermodynamik ein freiwillig ablaufender Prozess, der sich nicht ohne äußere Einwirkung umkehren lässt.
Die größere Entropie bei einer Verteilung über das gesamte Volumen ergibt sich auch aus der größeren Anzahl von Verteilungsmustern (oder Mikrozuständen), die die Teilchen bilden können, wenn sie mehr Platz zur Verfügung haben.[9][10] Die Anzahl der Mikrozustände, die denselben Makrozustand bilden, heißt sein statistisches Gewicht Ω {displaystyle Omega } . Damit hat eine großräumige Verteilung auch ein höheres statistisches Gewicht im Vergleich zu einer räumlich konzentrierten Anordnung und ist deshalb auch wahrscheinlicher. Die Entropie ( S = k ⋅ ln Ω {displaystyle S=kcdot ln Omega } ) eines Makrozustands ist somit ein Maß für dessen Wahrscheinlichkeit.
Analogie zur Wärmeleitung und Leitung von elektrischem Strom
Die Diffusion folgt Gesetzmäßigkeiten, die denen der Wärmeleitung[11] äquivalent sind. Daher kann man Gleichungen, die den einen Prozess beschreiben, für den anderen übernehmen.
Diffusion gelöster Teilchen
Bei festgelegtem Druck p {displaystyle p} und festgelegter Temperatur T {displaystyle T} ist aus dem Blickwinkel der Thermodynamik der Gradient des chemischen Potentials μ {displaystyle mu } die treibende Ursache des Stoffstroms. Der Fluss ergibt sich somit zu:
- J=−K(∂μ∂x)p,T{displaystyle J=-Kleft({frac {partial mu }{partial x}}right)_{p,T}}
- J{displaystyle J}: Teilchenstromdichte (Fluss) in mol · m−2 · s−1
- μ{displaystyle mu }: Chemisches Potential in J · mol−1
- x{displaystyle x}: Länge in m
- K{displaystyle K}: ein Koeffizient in mol2 · s · kg−1 · m−3
Für einfache Anwendungsfälle kann anstelle des chemischen Potentials die Stoffmengenkonzentration c {displaystyle c} verwendet werden. Diese ist einfacher zugänglich als das chemische Potential eines Stoffes. Für ein ideales Gas ist das chemische Potential gegeben durch
- μ=μ∘+RTln(cc∘){displaystyle mu =mu ^{circ }+RTln left({frac {c}{c^{circ }}}right)},
Dabei ist μ ∘ {displaystyle mu ^{circ }} das chemische Potential eines sinnvoll zu wählenden Referenzzustandes, bei dem es sich jedoch nicht um einen durch Vorliegen von Standardbedingungen gekennzeichneten Standard- oder Normzustand handeln muss.[12] Für einen nicht-idealen Stoff müssen zusätzliche Excess-Terme berücksichtigt werden, da Teilchenwechselwirkungen vorliegen (siehe Chemisches Potential). Hängt die Temperatur nicht explizit vom Ort ab, so gilt:
- ∂μ(x,t)∂x=∂μ∘∂x+∂RTln(c(x,t)/c∘)∂x=RT∂ln(c(x,t)/c∘)∂x=RTc∘c(x,t)∂c(x,t)/c∘∂x=RTc(x,t)∂c(x,t)∂x{displaystyle {frac {partial mu (x,t)}{partial x}}={frac {partial mu ^{circ }}{partial x}}+{frac {partial RTln(c(x,t)/c^{circ })}{partial x}}=RT{frac {partial ln(c(x,t)/c^{circ })}{partial x}}={frac {RTc^{circ }}{c(x,t)}}{frac {partial c(x,t)/c^{circ }}{partial x}}={frac {RT}{c(x,t)}}{frac {partial c(x,t)}{partial x}}}
Setzt man dieses in die obige Gleichung ein, erhält man das erste Ficksche Gesetz:
- J=−K∂μ∂x=−KRTc∂c∂x=−D∂c∂x{displaystyle J=-K{frac {partial mu }{partial x}}=-K{frac {RT}{c}}{frac {partial c}{partial x}}=-D{frac {partial c}{partial x}}}
Hierbei wurde der Diffusionskoeffizient D {displaystyle D} eingeführt. Der Zusammenhang der Koeffizienten K {displaystyle K} und D {displaystyle D} ist
- K=DcRT{displaystyle K={frac {Dc}{RT}}}
wobei
- D{displaystyle D}: Diffusionskoeffizient in m2 s−1
- c{displaystyle c}: Stoffmengenkonzentration in mol · m−3
- T{displaystyle T}: Temperatur in K
- R{displaystyle R}: Universelle Gaskonstante in J · K−1 · mol−1
Bei sehr geringen Konzentrationen (einzelne Moleküle) ist diese Betrachtung nicht mehr ohne weiteres zulässig, da die klassische Thermodynamik Lösungen als Kontinuum betrachtet. Bei hohen Konzentrationen beeinflussen sich die Teilchen gegenseitig, so dass bei anziehender Wechselwirkung der Konzentrationsausgleich langsamer, bei abstoßender schneller erfolgt. Das chemische Potential ist in diesen Fällen nicht mehr logarithmisch von der Konzentration abhängig.
Erstes Ficksches Gesetz
Nach dem Ersten Fickschen Gesetz ist die Teilchenstromdichte J {displaystyle J} proportional zum Konzentrationsgradienten ∂ c / ∂ x {displaystyle partial c/partial x} entgegen der Diffusionsrichtung. Die Proportionalitätskonstante ist der Diffusionskoeffizient D {displaystyle D} .
- J=−D∂c∂x{displaystyle J=-D{frac {partial c}{partial x}}}
Die Einheiten sind beispielsweise [ J ] {displaystyle [J]} = mol m−2 s−1, [ ∂ c / ∂ x ] {displaystyle [partial c/partial x]} = mol·m−4 und [ D ] {displaystyle [D]} = m2 s−1.
Die Teilchenstromdichte macht eine quantitative Aussage über die (im statistischen Mittel) gerichtete Bewegung von Teilchen, d. h. wie viele Teilchen einer Stoffmenge sich pro Zeit durch eine Fläche, die senkrecht zur Diffusionsrichtung liegt, netto bewegen. Die angegebene Gleichung gilt auch für den allgemeinen Fall, dass der Diffusionskoeffizient nicht konstant ist, sondern von der Konzentration abhängt (das ist aber streng genommen nicht mehr die Aussage des Ersten Fickschen Gesetzes).
Als Erweiterung des Fickschen Gesetzes kann die Nernst-Planck-Gleichung angesehen werden.
Zweites Ficksches Gesetz (Diffusionsgleichung)
Kontinuitätsgleichung und Differentialgleichung für den eindimensionalen Fall
Mit Hilfe der Kontinuitätsgleichung (Massenerhaltung)
- ∂c∂t=−∂J∂x{displaystyle {frac {partial c}{partial t}}=-{frac {partial J}{partial x}}}
ergibt sich aus dem Ersten Fickschen Gesetz die Diffusionsgleichung
- ∂c∂t=∂∂x(D∂c∂x),{displaystyle {frac {partial c}{partial t}}={frac {partial }{partial x}}left(D{frac {partial c}{partial x}}right),}
für konstante Diffusionskoeffizienten ergibt sich hieraus
- ∂c∂t=D∂2c∂x2{displaystyle {frac {partial c}{partial t}}=D{frac {partial ^{2}c}{partial x^{2}}}}.
Sie stellt eine Beziehung zwischen zeitlichen und örtlichen Konzentrationsunterschieden dar und eignet sich somit zur Darstellung instationärer Diffusion, im Gegensatz zum 1. Fickschen Gesetz, das einen zeitlich konstanten Diffusionsfluss beschreibt. Es existieren für diese Differentialgleichung zahlreiche analytische und numerische Lösungsansätze, die jedoch stark von den Anfangs- und Randbedingungen abhängen.
Mathematisch gesehen ist die Diffusionsgleichung identisch mit der Wärmeleitungsgleichung, ihre mathematischen Eigenschaften und Lösungsansätze werden im dortigen Artikel behandelt.
Differentialgleichung für den dreidimensionalen Fall
Der Fall der dreidimensionalen Diffusion lässt sich mit dem Zweiten Fickschen Gesetz in seiner allgemeinsten Form beschreiben:
- ∂c∂t=∇⋅(D∇c){displaystyle {frac {partial c}{partial t}}=nabla cdot left(Dnabla cright)}
mit dem Nabla-Operator ∇ {displaystyle nabla } . Mathematisch gesehen ist auch diese Diffusionsgleichung identisch mit der (dreidimensionalen) Wärmeleitungsgleichung, ihre mathematischen Eigenschaften und Lösungsansätze werden im dortigen Artikel behandelt. Die Lösung dieser Gleichung ist in der Regel aufwändig und je nach betrachtetem Gebiet nur numerisch möglich.
Im stationären Fall, d. h. für
- ∂c∂t=0{displaystyle {frac {partial c}{partial t}}=0}
ergibt sich die elliptische partielle Differentialgleichung
- 0=∇⋅(D∇c).{displaystyle 0=nabla cdot left(Dnabla cright).}
Wenn nun zusätzlich der Diffusionskoeffizient isotrop ist, erhält man eine Differentialgleichung vom Laplace-Typ.
Ist neben der Diffusion auch ein gerichteter Transport beteiligt, so wird die Konzentrationsdynamik durch die Konvektions-Diffusions-Gleichung beschrieben.
Arten von Diffusion
Es ist üblich, vier Arten der Diffusion zu unterscheiden.[13] Die Diffusionskoeffizienten unterscheiden sich bei unterschiedlichen Diffusionsarten, auch wenn gleiche Teilchen unter Standardbedingungen diffundieren.
Selbstdiffusion
Wenn in einem Gas, einer reinen Flüssigkeit oder einer Lösung kein makroskopischer Gradient existiert, findet ausschließlich echte Selbstdiffusion (engl.: self diffusion) statt. Selbstdiffusion (oft auch als Intradiffusion bezeichnet) ist der Transport von Teilchen innerhalb derselben Substanz, beispielsweise Wassermoleküle in reinem Wasser oder Natriumionen in einer NaCl-Lösung. Da dieses wegen der schwierigen Unterscheidbarkeit physikalisch und chemisch gleicher Teilchen allenfalls mit großem Aufwand zu beobachten ist, nähert man Selbstdiffusion oft mit isotopischen Tracern desselben Stoffes an, beispielsweise 22Na+ für Natriumionen. Dabei geht man davon aus, dass der Gradient, der durch Zugabe des Tracers entsteht, vernachlässigbar klein ist. Selbstdiffusion ist ein Modell zur Beschreibung der Brownschen Molekularbewegung. Die gemessenen Diffusionskoeffizienten lassen sich über σ 2 = 2 D {displaystyle sigma ^{2}=2D} in die mittlere quadratische Verschiebung eines Teilchens pro Zeitspanne umrechnen.[7]
Eine besonders geeignete Methode zur Messung von Selbstdiffusionskoeffizienten stellt die Feldgradienten-NMR dar. Hier werden keine isotopischen Tracer benötigt, da physikalisch und chemisch gleiche Teilchen mittels der Kernspin-Präzessionsphase eines im Teilchen befindlichen Atomkerns unterscheidbar werden. Mit dieser NMR-Technik können sowohl Selbstdiffusionskoeffizienten in reinen Flüssigkeiten, wie auch in komplexen, fluiden Gemischen sehr präzise ermittelt werden.[14] Der Selbstdiffusionskoeffizient des reinen Wassers wurde äußerst genau gemessen und dient daher häufig als Referenzwert. Er beträgt 2,299·10−9 m²·s−1 bei 25 °C und 1,261·10−9 m²·s−1 bei 4 °C.[15]
Tracerdiffusion
Tracerdiffusion ist die Diffusion geringer Konzentrationen eines Stoffes in einer Lösung einer zweiten Substanz. Tracerdiffusion unterscheidet sich von der Selbstdiffusion dahingehend, dass ein markiertes Teilchen eines anderen Stoffes als Tracer benutzt wird, z. B. 42K+ in NaCl-Lösung. Häufig werden radioaktiv oder fluoreszenzmarkierte Tracer verwendet, da man diese sehr gut detektieren kann. Bei unendlicher Verdünnung sind die Diffusionskoeffizienten von Selbst- und Tracerdiffusion identisch.
Klassische Ficksche Diffusion
Dies bezeichnet die Diffusion entlang eines relativ starken Gradienten. Bei dieser Art der Diffusion ist eine Approximation des Diffusionskoeffizienten am besten möglich.
Gegendiffusion
Gegendiffusion (engl.: counter diffusion) tritt auf, wenn entgegengesetzte Gradienten vorhanden sind, so dass Teilchen in entgegengesetzte Richtungen diffundieren.
Diffusion von Gasen
Prinzipiell unterscheidet sich die Diffusion von Teilchen in Gasen hinsichtlich ihrer Gesetzmäßigkeiten nicht von der Diffusion gelöster Teilchen in Flüssigkeiten. Allerdings ist die Geschwindigkeit der Diffusion (bei vergleichbaren Gradienten) hier um Größenordnungen höher, da auch die Bewegung einzelner Teilchen in Gasen erheblich schneller ist. Die Diffusion verdünnter Gase in Multikomponentensystemen lässt sich mit dem Modell der Maxwell-Stefan-Diffusion beschreiben.
Diffusion in Festkörpern
In einem perfekten Kristallgitter schwingt jedes Gitterteilchen um seinen festen Gitterplatz und kann diesen nicht verlassen. Eine notwendige Voraussetzung für Diffusion in einem kristallinen Festkörper ist daher das Vorliegen von Gitterfehlstellen. Nur durch diese Bedingung können Platzwechsel von Atomen oder Ionen, und damit ein Stofftransport stattfinden. Es sind verschiedene Mechanismen denkbar:[16]
- Die Teilchen „springen“ in Leerstellen des Gitters, sodass sich Leerstellen durch das Gitter bewegen und ein Nettofluss von Teilchen stattfindet. Dieser Mechanismus wurde durch den Kirkendall-Effekt nachgewiesen.
- Kleinere Teilchen bewegen sich durch die Gitterzwischenräume. Er führt im Vergleich zur Diffusion über Leerstellen zu sehr hohen Diffusionskoeffizienten. Auch dieser Mechanismus wurde experimentell nachgewiesen.
- Zwei Teilchen tauschen die Plätze oder es finden Ringtausche zwischen mehreren Teilchen statt. Dieser hypothetische Mechanismus konnte experimentell bisher nicht bestätigt werden.
- Falls freie Ladungsträger in Halbleitern hinreichend viel Streuung erfahren (z. B. an Phononen, Elektronen und Störstellen), propagieren sie ebenfalls diffusiv.
Auch die Diffusion in Kristallen lässt sich durch die Fickschen Gesetze beschreiben. Allerdings können Diffusionskoeffizienten hier von der Raumrichtung abhängen (Anisotropie). Die im isotropen Fall skalaren Diffusionskoeffizienten werden dann zu einem Tensor zweiter Stufe, genannt Diffusionstensor. Deshalb ist der Diffusionsweg eine wichtige Größe zur Beschreibung von Diffusionsvorgängen in Festkörpern.
Im Falle von Anisotropie schreibt sich beispielsweise das erste Ficksche Gesetz wie folgt:
- j→=−D¯¯∇c{displaystyle {vec {j}}=-{overline {overline {D}}}nabla c,}
in dem nun
- D¯¯=[DxDxyDxzDyxDyDyzDzxDzyDz]{displaystyle {overline {overline {D}}}={begin{bmatrix}D_{x}&D_{xy}&D_{xz}D_{yx}&D_{y}&D_{yz}D_{zx}&D_{zy}&D_{z}end{bmatrix}}}
eine 3×3-Matrix ist, die als Diffusions-Tensor (oder Diffusionsmatrix) bezeichnet wird. Diese Matrix ist symmetrisch und hat daher jedoch nur sechs unabhängige Komponenten.
Die Diffusion in nichtkristallinen (amorphen) Festkörpern ähnelt in mechanistischer Hinsicht der in Kristallen, wobei allerdings die Unterscheidung zwischen regulären und irregulären Gitterplätzen entfällt. Mathematisch können solche Prozesse gut wie die Diffusion in Flüssigkeiten beschrieben werden.
Fokker-Planck-Gleichung
Eine zusätzliche treibende Größe durch ein vorhandenes Potential führt dazu, dass die Gleichverteilung nicht mehr dem stationären Zustand entspricht. Die Theorie dazu liefert die Fokker-Planck-Gleichung.
Sonderfall: Anomale Diffusion
Bei den vorstehend beschriebenen Diffusionsprozessen, die durch die Ficksche Diffusionsgleichung beschrieben werden können, steigt die mittlere quadratische Auslenkung ⟨ Δ x 2 ⟩ ( t ) {displaystyle langle Delta x^{2}rangle (t)} der diffundierenden Teilchen (also der mittlere Abstand der Teilchen zu ihrem Startpunkt nach der Zeit t {displaystyle t} ) proportional zur Zeit an:
- ⟨Δx2⟩(t)∝t{displaystyle langle Delta x^{2}rangle (t)propto t}
Diese Gesetzmäßigkeit folgt aus der Theorie der Brown’schen Molekularbewegung. In Zellen können aber auch andere Gesetzmäßigkeiten beobachtet werden, beispielsweise bei der Bewegung von Makromolekülen durch das Cytoplasma der Zelle. Dieses mit Organellen und (Makro)molekülen dicht besetzte Medium führt zu einer gebremsten Diffusionsbewegung, die einem Potenzgesetz folgt. Es gilt dann:
- ⟨Δx2⟩(t)∝tα{displaystyle langle Delta x^{2}rangle (t)propto t^{alpha }}
Für diese gebremste Bewegung, die Subdiffusion genannt wird, gilt 0 < α < 1 {displaystyle 0<alpha <1} .[17] Es existieren auch Diffusionsprozesse, bei denen α > 1 {displaystyle alpha >1} ist, die also beschleunigt sind. Diese werden als Superdiffusion bezeichnet.
Sonderfall: Erleichterte Diffusion (Biologie)
Die erleichterte Diffusion oder Permeabilität beschreibt in der Biologie die Möglichkeit für bestimmte Stoffe, eine Biomembran leichter zu durchdringen, als dies eigentlich aufgrund ihrer Größe, Ladung, Polarität etc. möglich wäre. Bestimmte Proteine, sogenannte Tunnelproteine, bilden einen Tunnel durch die Zellmembran, der durch seinen Durchmesser und/oder seine Ladungsverteilung bestimmte Stoffe leichter passieren lässt als durch die „geschlossene“ Membran (etwa Ionenkanäle).
Falsche Wortanwendung von Diffusion
Die Begriffe Diffusion und Diffusivität werden auf dem Gebiet der Akustik häufig statt des deutschen Wortes Diffusität verwendet. Die falsche Übersetzung aus dem Englischen trägt dazu bei.
Siehe auch
- Reaktions-Diffusionsgleichung
- Eddy-Diffusion, bezeichnet Vermischung durch Strömung
- Knudsen-Diffusion, durch Begrenzungen dominierte Diffusion
- Kritische Schichtdicke
- Lévy-Prozess
- Diffusionsnetz
- Diffusivität
- Neutronendiffusion
- Transepidermaler Wasserverlust
Literatur
- Peter W. Atkins, Charles A. Trapp: Physikalische Chemie. 3. korrigierte Auflage. Wiley-VCH, Weinheim u. a. 2001, ISBN 3-527-30236-0.
- Klopfer, H.: Wassertransport durch Diffusion in Feststoffen. Wiesbaden: Bauverlag 1974 (Abstract).
- E. L. Cussler: Diffusion. Mass Transfer in Fluid Systems. 2nd edition. Cambridge University Press, Cambridge u. a. 1997, ISBN 0-521-56477-8.
- J. Crank: The Mathematics of Diffusion. 2nd revised edition. Oxford University Press, Oxford u. a. 1980, ISBN 0-19-853411-6.
- Paul Heitjans, Jörg Kärger (Hrsg.): Diffusion in Condensed Matter. Methods, Materials, Models. Greatly enlarged and completely revised edition. Springer, Berlin u. a. 2005, ISBN 3-540-20043-6.
- Jörg Kärger (Hrsg.): Leipzig, Einstein, Diffusion. Leipziger Universitätsverlag, Leipzig, 2007, (3. Auflage 2014), ISBN 978-3-86583-176-7.
- Wilhelm Jost: Diffusion in solids, liquids, gases (= Physical chemistry 1, ISSN 0079-1881). 6th printing. Academic Press, New York NY 1970.
- H. J. V. Tyrrell, K. R. Harris: Diffusion in Liquids. A theoretical and experimental Study. Butterworth, London 1984, ISBN 0-408-17591-5.
Weblinks
- Die Fickschen Diffusionsgesetze, H. Föll, Technische Fakultät der Christian-Albrechts-Universität zu Kiel
- Diffusion in Physikalische Werkstoffeigenschaften (PDF-Datei, 160 kB) beim Leibniz-Institut für Festkörper- und Werkstoffforschung
- 3D-Gitter-Monte-Carlo-Simulation der Diffusion auf einer vizinal geschnittenen kfz-(100)-Oberfläche von Lars Röntzsch
- NetLogo-Simulationsmodell für den Unterricht (Java-Applet) von Johannes Kottonau
- Video: Diffusion und Ficksche Gesetze – wie schnell geht Stofftransport ohne Strömung?. Jakob Günter Lauth (SciFox) 2013, zur Verfügung gestellt von der Technischen Informationsbibliothek (TIB), doi:10.5446/15654.

 -dimensionalen Raum mit der n {displaystyle n}
-dimensionalen Raum mit der n {displaystyle n}  (Subskript S steht für Selbstdiffusion) ist eine Funktion der Zeit.
(Subskript S steht für Selbstdiffusion) ist eine Funktion der Zeit.
 herrscht die Kurzzeitdiffusionskonstante D S k = lim t → τ 0 D S ( t ) {displaystyle D_{text{S}}^{text{k}}=lim _{tto tau _{0}}D_{text{S}}(t)}
herrscht die Kurzzeitdiffusionskonstante D S k = lim t → τ 0 D S ( t ) {displaystyle D_{text{S}}^{text{k}}=lim _{tto tau _{0}}D_{text{S}}(t)}  vor.
vor. .
. eines Teilchens in der Zeit τ für den eindimensionalen Fall zu ⟨ r 2 ( τ ) ⟩ = 2 D τ {displaystyle langle r^{2}(tau )rangle =2Dtau }
eines Teilchens in der Zeit τ für den eindimensionalen Fall zu ⟨ r 2 ( τ ) ⟩ = 2 D τ {displaystyle langle r^{2}(tau )rangle =2Dtau }  . Kurze Zeit nach Einstein kam Smoluchowski auf einem anderen Weg ebenfalls zu praktisch derselben Beziehung, und daher wird diese Gleichung heute als Einstein-Smoluchowski-Gleichung bezeichnet.
. Kurze Zeit nach Einstein kam Smoluchowski auf einem anderen Weg ebenfalls zu praktisch derselben Beziehung, und daher wird diese Gleichung heute als Einstein-Smoluchowski-Gleichung bezeichnet.


 . Damit hat eine großräumige Verteilung auch ein höheres statistisches Gewicht im Vergleich zu einer räumlich konzentrierten Anordnung und ist deshalb auch wahrscheinlicher. Die Entropie ( S = k ⋅ ln Ω {displaystyle S=kcdot ln Omega }
. Damit hat eine großräumige Verteilung auch ein höheres statistisches Gewicht im Vergleich zu einer räumlich konzentrierten Anordnung und ist deshalb auch wahrscheinlicher. Die Entropie ( S = k ⋅ ln Ω {displaystyle S=kcdot ln Omega }  ) eines Makrozustands ist somit ein Maß für dessen Wahrscheinlichkeit.
) eines Makrozustands ist somit ein Maß für dessen Wahrscheinlichkeit. und festgelegter
und festgelegter  ist aus dem Blickwinkel der
ist aus dem Blickwinkel der  die treibende Ursache des Stoffstroms. Der Fluss ergibt sich somit zu:
die treibende Ursache des Stoffstroms. Der Fluss ergibt sich somit zu:
 :
:  :
:  : ein Koeffizient in mol2 · s · kg−1 · m−3
: ein Koeffizient in mol2 · s · kg−1 · m−3 verwendet werden. Diese ist einfacher zugänglich als das chemische Potential eines Stoffes. Für ein ideales Gas ist das chemische Potential gegeben durch
verwendet werden. Diese ist einfacher zugänglich als das chemische Potential eines Stoffes. Für ein ideales Gas ist das chemische Potential gegeben durch ,
, das chemische Potential eines sinnvoll zu wählenden
das chemische Potential eines sinnvoll zu wählenden 

 eingeführt. Der Zusammenhang der Koeffizienten K {displaystyle K}
eingeführt. Der Zusammenhang der Koeffizienten K {displaystyle K} 
 :
:  entgegen der Diffusionsrichtung. Die Proportionalitätskonstante ist der
entgegen der Diffusionsrichtung. Die Proportionalitätskonstante ist der 
![{displaystyle [J]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/50de4527394eeac6ace20edb789515c595c2c73a) = mol m−2 s−1, [ ∂ c / ∂ x ] {displaystyle [partial c/partial x]}
= mol m−2 s−1, [ ∂ c / ∂ x ] {displaystyle [partial c/partial x]} ![{displaystyle [partial c/partial x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e0b90485811ae81287050bb8eb1634023b05290f) = mol·m−4 und [ D ] {displaystyle [D]}
= mol·m−4 und [ D ] {displaystyle [D]} ![{displaystyle [D]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1c4bcb25d77a0de74082c849178200b8cf1340b4) = m2 s−1.
= m2 s−1.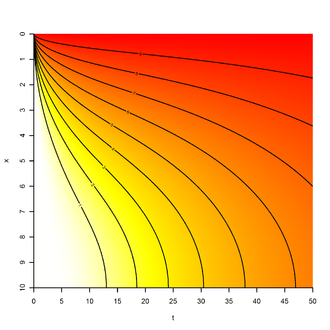


 .
.
 . Mathematisch gesehen ist auch diese Diffusionsgleichung identisch mit der (dreidimensionalen)
. Mathematisch gesehen ist auch diese Diffusionsgleichung identisch mit der (dreidimensionalen) 

 in die mittlere quadratische Verschiebung eines Teilchens pro Zeitspanne umrechnen.
in die mittlere quadratische Verschiebung eines Teilchens pro Zeitspanne umrechnen.





 der diffundierenden Teilchen (also der mittlere Abstand der Teilchen zu ihrem Startpunkt nach der Zeit t {displaystyle t}
der diffundierenden Teilchen (also der mittlere Abstand der Teilchen zu ihrem Startpunkt nach der Zeit t {displaystyle t}  ) proportional zur Zeit an:
) proportional zur Zeit an:

 .
. ist, die also beschleunigt sind. Diese werden als Superdiffusion bezeichnet.
ist, die also beschleunigt sind. Diese werden als Superdiffusion bezeichnet.