|
|
|
Jörn Loviscach (* 1965) ist Professor für Ingenieurmathematik und technische Informatik an der Fachhochschule Bielefeld [1] sowie ehemaliger stellvertretender Chefredakteur der Computer-Zeitschrift c’t.[2] Loviscach ist Themenpate der Themengruppe „Innovationen in Lern- und Prüfungsszenarien“ beim 2014 vom Centrum für Hochschulentwicklung, Hochschulrektorenkonferenz und Stifterverband initiierten Hochschulforum Digitalisierung, welches vom Bundesministerium für Bildung und Forschung gefördert wird.[3]
Inhaltsverzeichnis
Forschung[Bearbeiten | Quelltext bearbeiten]
Loviscach wurde 1993 an der Universität Bielefeld promoviert, der Titel der Dissertation lautete Probabilistic models of chaotic maps.[4] Des Weiteren veröffentlichte er Beiträge zu diesem Forschungsgebiet in der Schriftenreihe des Forschungszentrums Bielefeld-Bochum-Stochastik (A large class of functions with good properties under Anosov maps, 1993) sowie in den Fachzeitschriften Journal of Statistical Physics (Band 75, 1994, S. 189–213) und Probability Theory and Related Fields (Band 103, 1995, S. 553–570).
Von März 2005 bis August 2008 leitete er am Institut für Informatik und Automation der Hochschule Bremen das Forschungsprojekt ViSE: Virtual Sound Engineer, bei dem es um die Entwicklung medialer Hilfsmittel zur Arbeit mit Audiodaten ging.[5] Loviscach beschäftigt sich auch mit der Gestaltung von Benutzerschnittstellen bei Computerspielen (Advances in Computers, Band 77, 2009, S. 79–115).
Lehre[Bearbeiten | Quelltext bearbeiten]
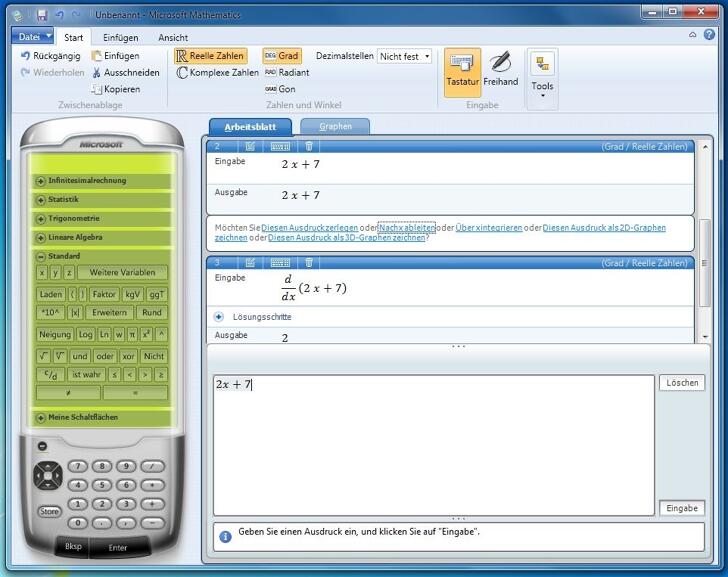
Bekanntheit erlangte er unter anderem dadurch, dass er seine gefilmten Vorlesungen auf dem Videoportal YouTube zur Verfügung stellt und diese Aufzeichnungen in seinen Unterricht integriert.[6] Zu seinen Lehrkonzepten zählt auch die Unterrichtsmethode des inverted teaching.[7] Der Kanal von Jörn Loviscach hat mittlerweile eine Zugriffszahl von mehr als 15 Millionen Aufrufen, über 50.000 Abonnenten und ca. 2700 Videos.[8][9][10] Die von ihm benutzten technischen Hilfsmittel umfassen dabei einen Tablet-PC, auf dem er mit einem Touchpen schreiben sowie zeichnen kann und von dem das Bild durch einen Beamer an die Wand projiziert wird.[11] Die Videos auf Youtube können auch auf der eigenen Internetseite von Jörn Loviscach sortiert und per Suchmaschine abgerufen und angeschaut werden.[12]
Zu den Nutzungsmöglichkeiten von YouTube im Unterricht hielt er im September 2011 auf der Tagung der Fachgruppe E-Learning in der Gesellschaft für Informatik (DeLFI 2011) einen Vortrag zum Thema Mathematik auf YouTube: Herausforderungen, Werkzeuge, Erfahrungen.[13] Auf Udacity unterrichtet er den Online-Kurs „Making Math Matter: Differential Equations in Action“.[14]
Seit Dezember 2012 erstellt Loviscach Videos unter dem Titel „Reisen durch die Raumzeit“, in denen er dem Zuschauer unter mathematischen Gesichtspunkten die Physik der Allgemeinen und Speziellen Relativitätstheorie aufzeigt.
Wissenschaftliche Veröffentlichungen (Auswahl)[Bearbeiten | Quelltext bearbeiten]
- 2004 Shader Programming: An Introduction Using the Effect Framework, Revista de Informática Teórica e Aplicada, (Band 11, Nummer 1, S. 125–164)
- 2004 Stylized haloed outlines on the GPU, Proceeding SIGGRAPH ’04 ACM SIGGRAPH 2004 Posters, Seite 92
- 2005 Efficient magnification of bi-level textures, Proceeding SIGGRAPH ’05 ACM SIGGRAPH 2005 Sketches, Article No. 131
- 2006 Wrinkling Coarse Meshes on the GPU, Computer Graphics Forum 25(3), S. 467–476.
- 2006 subjEQt: controlling an equalizer through subjective terms, Proceeding CHI EA06, extended abstracts on Human factors in computing systems, S. 1109–1114
- 2007 Two-finger input with a standard touch screen, Proceeding UIST’07 20th annual ACM symposium on User interface software and technology, S. 169–172
- 2008 P. Kolhoff, J. Preuß, J.L.: Content-Based Icons for Music Files. Computers & Graphics 32, S. 550–560
Trivia[Bearbeiten | Quelltext bearbeiten]
Gesprochen wird der Name „Lowischach“ mit Betonung auf dem „o“.
Weblinks[Bearbeiten | Quelltext bearbeiten]
Listen mit Skripten und Material, zusammengefasst aus allen Jahren:
Videos zum Download mit eingerenderten Anmerkungen und Korrekturen, mit verbessertem Transkript und mit Nachtmodus:
http://www.j3L7h2.de/videos/p.html
Technik hinter diesen Videos
Die Links unten verlassen diese Seite; sie führen zu www.youtube.com. Die Zahlen mit Ausrufezeichen hinter einigen Videos geben nachträgliche Anmerkungen an; für Details die Maus über die Zahlen halten. Die Anmerkungen sind beim Abspielen eines Videos im Webbrowser als Sprechblasen sichtbar, fehlen derzeit allerdings in den YouTube-Apps für mobile Geräte.
Video suchen:
Zum Beispiel: Integral, Vektorprodukt, for-Schleife
Playlists
- Einführungswochen 2011
- Experimente
- Favorites
- Gebäudeautomation, Sommer 2015
- Informatik 1, Winter 2010/2011
- Informatik 1, Winter 2011/2012
- Informatik 1, Winter 2012/2013
- Informatik 1, Winter 2013/2014
- Informatik 1, Winter 2014/2015
- Informatik 2, Sommer 2011
- Informatik 2, Sommer 2012
- Informatik 2, Sommer 2013
- Informatik 2, Sommer 2014
- Informatik 2, Sommer 2015
- Informatik 2, Sommer 2016
- Informatik 2, Sommer 2017
- Mathe 1 Teil 1, Winter 2010/2011
- Mathe 1 Teil 2, Winter 2010/2011
- Mathe 1, Winter 2011/2012
- Mathe 1, Winter 2012/2013
- Mathe 1, Winter 2013/2014
- Mathe 1, Winter 2015/2016
- Mathe 1, Winter 2016/2017
- Mathe 2 Teil 1, Sommer 2010
- Mathe 2 Teil 2, Sommer 2010
- Mathe 2, Sommer 2011
- Mathe 2, Sommer 2012
- Mathe 2, Sommer 2013
- Mathe 2, Sommer 2014
- Mathe 2, Sommer 2015
- Mathe 2, Sommer 2016
- Mathe 2, Sommer 2017
- Mathe-Vorkurs 2013
- Mensch-Maschine-Interaktion Winter 2013/2014
- Mensch-Maschine-Interaktion Winter 2014/2015
- Mensch-Maschine-Interaktion Winter 2015/2016
- Mensch-Maschine-Interaktion Winter 2016/2017
- Projekt Solarprognose
- Reisen durch die Raumzeit
- Spezialthemen
- Talks and Demos
- Udacity CS222 Highlights
- Wind- und Wasserkraft, Winter 2014/2015
- Wind- und Wasserkraft, Winter 2015/2016
- Wind- und Wasserkraft, Winter 2016/2017
Einführungswochen 2011
8:22:47
- 01 Windows-Taschenrechner, Standardfunktionen, Grad und Radiant, Verlauf 16:55
- 02 Wolfram Alpha, Teil 1, Plots, Gleichungen, Ungleichungen, Ableitungen, Integrale 14:45
- 03 Wolfram Alpha, Teil 2, Extrema, Genauigkeit, Vektorrechnung, Einheiten 15:10
- 04 MATLAB (R), Teil 1, Rechnen mit Zahlen, Variablen, Vektorrechnung, Plots 18:38
- 05 MATLAB (R), Teil 2, Skripte (.m-Dateien), Fehlerbalken, Computeralgebra 11:17
- 05a MATLAB(R), Teil 3, Funktionen definieren, komponentenweise Multiplikation und Potenzierung 14:38
- 06 OpenOffice.org Calc, Teil 1, Tabellen, Auswählen, Formatierung, Füllen 13:52
- 07 OpenOffice.org Calc, Teil 2, Verweise, Füllen mit Formeln 14:23
- 08 OpenOffice.org Calc, Teil 3, Sortieren, Diagramme, Regressionsgerade (Trendlinie), Fehlerbalken 16:07
- 09 OpenOffice.org Calc, Teil 4, Diagramme ausgeben, Bereiche, Formatvorlagen, Autoformat 13:59
- 10 Google Docs Tabellen, Freigabe, Chat, Formeln, Diagramme 13:11
!1 - 11 OpenOffice.org Writer, Teil 1, Anführungszeichen, Gedankenstrich, Zeilenumbruch 23:44
- 12 OpenOffice.org Writer, Teil 2, Absatzformatvorlagen, Zeilenabstand, Erstzeileneinzug 16:41
- 13 OpenOffice.org Writer, Teil 3, Silbentrennung, Absatzkontrolle, Seitenanfang pro Kapitel 11:58
- 14 OpenOffice.org Writer, Teil 4, Listen, Gliederungsnummerierung, Inhaltsverzeichnis 13:39
- 15 OpenOffice.org Writer, Teil 5, Kopfzeile, Fußzeile, Seitennummer, doppelseitig 18:34
- 16 OpenOffice.org Writer, Teil 6, Bilder, Querverweise, Literaturverzeichnis, Änderungen verfolgen 12:11
- 17 Google Docs Text, Kommentare, Bearbeitungsverlauf 4:17
- 18 Inkscape, Teil 1, Vektorgrafik versus Bitmaps, SVG, PDF, WMF, JPG, PNG, BMP, Seitenformat 15:21
- 19 Inkscape, Teil 2, Rechteck, Ellipse, Kreis, Stern, Vieleck, Spirale, Freihandlinie 15:16
- 20 Inkscape, Teil 3, Füllung, Farbverlauf, Muster, Konturlinie 23:27
- 21 Inkscape, Teil 4, Pfade, Bézier-Kurven editieren, Boolesche Operationen, Text 12:10
- 22 Inkscape, Teil 5, Gitter, Hilfslinien, Einrasten, Ausrichten, Verteilen, Gruppieren, Ebenen 16:02
- 22a Diagramme mit yEd und mit LucidChart 7:56
- 23 Gimp, Teil 1, JPEG, Artefakte, PNG, Screenshots machen 25:39
- 24 Gimp, Teil 2, Navigation, Zoom, Farben, Pinsel, Airbrush, Malmodi 12:14
- 25 Gimp, Teil 3, Weichzeichnen, Scharfzeichnen, Kunstfilter 10:23
- 26 Gimp, Teil 4, Auswahl, Maskierung, Einfärben, Tilt Shift 21:43
- 27 Gimp, Teil 5, Stempel = Klonen, Perspektivkorrektur, Gradationskurven, Bildgröße, Ebenen 15:11
- 28 TeX, Teil 1, TeXnicCenter, MikTeX, SumatraPDF 21:00
- 29 TeX, Teil 2, LaTeX-Anweisungen, Formeln, Bilder, Tabellen, Querverweise, Inhaltsverzeichnis 31:56
!1!2!3 - 30 TeX, Teil 3, Literaturangaben mit BibTeX 10:30
Experimente
0:18:50
Favorites
15:19:05
- English Pronunciation – „The Chaos“ by Dr. Gerard Nolst Trenité 5:27
- robert bjork – desirable difficulties: slowing down learning 5:43
- This Will Revolutionize Education 7:23
- A Postmodern Mathematics Education .avi 14:17
- Research-based principles for multimedia learning 1:24:28
- TEDxManhattanBeach – John Bennett – Why Math Instruction Is Unnecessary 11:50
- Suli Breaks – Why I Hate School But Love Education [Official Spoken Word Video] 6:08
- TEDxDirigo – Zoe Weil – The World Becomes What You Teach 17:25
- Why Most Published Research Findings Are False 14:51
- STOP STEALING DREAMS: Seth Godin at TEDxYouth@BFS 16:58
- Education For Whom and For What? 1:59:28
- Confessions of a Converted Lecturer: Eric Mazur 1:20:09
- Seth Godin on Education 4:36
- TEDxEastsidePrep – Shawn Cornally – The Future of Education Without Coercion 17:20
- WHERE GOOD IDEAS COME FROM by Steven Johnson 4:07
- Alfie Kohn – The Case Against Competition 55:17
- 28c3: Security Nightmares (german) 1:33:14
- 28c3: The coming war on general computation 54:35
- Bernard Lietaer: Money diversity 23:39
- TEDxNYED – Gary Stager – 03/05/2011 16:37
- TEDxNYED – Jeff Jarvis – 03/06/10 16:25
- Study argues for drawing to be put back on the science curriculum 4:02
- SIGGRAPH 2011 : Cory Doctorow’s Keynote Address 46:28
- TEDxCaltech – Sanjoy Mahajan – Rote Learning Fragments the World 10:15
- Pi Is (still) Wrong. 5:17
- The transformative power of classical music | Benjamin Zander 20:44
- re:publica 2011 Gunter Dueck – Das internet als Gesellschaftsbetriebssystem 48:31
- TEDxCaltech – Leonard Susskind – Richard Feynman 15:42
- The call to learn | Clifford Stoll 17:51
- „Don’t lecture me“ – Donald Clark at ALT-C 2010 1:01:15
- Interaction Design 2:46
- Doodling in Math Class: Infinity Elephants 4:36
- RSA ANIMATE: Changing Education Paradigms 11:41
Gebäudeautomation, Sommer 2015
12:36:20
- Gebäudeautomation; Überblick 12:49
- Gebäudeautomation; Definition, Struktur 15:02
!1 - Gebäudeautomation wozu und wie 6:10
- Energieeinsparung durch Gebäudeautomation 24:41
- Gebäudeautomation, was braucht der Mensch 8:32
- Temperatur und Behaglichkeit 26:49
- Luftfeuchtigkeit 9:51
!1 - CO2 und andere Schadstoffe in der Luft 14:17
!1!2 - CO2 in Raumluft ohne und mit Lüften; Beispielrechnung 8:30
- Schall durch Lüftung 3:44
- Heizlastberechnung 20:33
!1 - Heizlast, Beispielrechnung 13:54
- Heizlast; Außenfläche im Verhältnis zum Volumen 3:53
- Warmwasserbedarf 4:11
- einfacher Heizkreis 3:33
- Brennwertkessel 9:19
!1!2!3 - Heizflächen, Heizkörper 7:15
!1 - Pumpenkennlinie, Anlagenkennlinie der Heizung 15:10
!1!2 - Heizleistung und Pumpenleistung 12:25
- Stellventil, Durchflussfaktor, Hub 14:15
!1!2 - Regelung der Pumpen-Warmwasserheizung 10:12
- Heizkurve 22:33
- Umwälzpumpe regeln 7:57
!1 - Hydraulik, Stellventil und Heizkörper, Teil 1 6:58
- Hydraulik, Stellventil und Heizkörper, Teil 2 28:28
!1 - Raumlufttechnik; Begriffe; Größenordnungen 17:33
!1!2 - Feuchte Luft; h,x-Diagramm 39:25
!1!2!3 - Feuchtegehalt und relative Luftfeuchtigkeit im h,x-Diagramm 28:28
- Geräte der Raumlufttechnik im h,x-Diagramm 17:11
!1 - Heizleistung und Luftfeuchtigkeit beim Erwärmen 15:36
- Enthalpieänderung durch Dampfbefeuchtung 25:12
- Kühlung mit Entfeuchtung 20:56
- Regelstrategie der Klimaanlage 7:05
- Grundaufbau der Klimaanlage 9:42
- Diagramme in der Gebäudeautomation 8:15
- Grundzüge der Regelung einer Klimaanlage 19:59
!1!2!3!4!5 - P- und PI-Regler; Einstellung nach Ziegler-Nichols 25:40
!1 - P-Regler, Kennlinien noch einmal im Detail 17:58
- Kaskadenregelung; Stellregler; Dreipunktregler 21:29
!1 - Regelung für Teilklimaanlage mit Wärmerückgewinnung 16:48
- Regelung einer Solaranlage mit Pufferspeicher 12:07
- Raumautomation 12:14
- Assistenzfunktionen von Gebäuden; AAL 4:46
!1 - Smart Home 1:59
- Wärmeleitungsgleichung; Schichtenspeicher 53:01
- Regelung einer Low-Flow-Solaranlage 10:42
!1 - Begriff Bus in der Gebäudeautomation 6:41
- KNX 6:30
!1 - BACnet 2:05
- Heimautomation 8:52
!1 - Grundlagen der SPS (speicherprogrammierbare Steuerung) 23:23
!1!2 - Mensch-Maschine-Schnittellen in der Gebäudeautomation 11:42
Informatik 1, Winter 2010/2011
19:23:19
- S01 TI LaunchPad, erstes Programm 10:45
- S02 MATLAB(R), erstes Programm 5:09
- 01.01 Was ist ein Computer? 7:05
- 01.02 Binärsystem, Bit 5:17
- 01.03.1 Byte, Kilobyte 5:50
- 01.03.2 weiter Byte, Kilobyte 7:55
- 01.04 PC versus Embedded 10:05
- 01.05.1 C, Variablen, Typen 10:45
- 01.05.2 weiter C, Variablen, Typen 4:34
- 01.06.1 if-Verzweigung 10:22
- 01.06.2 weiter if-Verzweigung 1:47
- 01.07.1 while-Schleife 8:22
- 01.07.2 weiter while-Schleife, Endlosschleife 4:09
- 02.01 Zahlensysteme in C 8:51
- 02.02.1 Operatoren in C 10:14
- 02.02.2 Operatoren in C, Short Circuit, Präzedenz 10:13
!1 - 02.03 Inkrement, Dekrement, Compound Assignment 4:58
- 02.04.1 Zoo der Programmiersprachen 8:42
!1 - 02.04.2 JavaScript, PHP, BASIC, Assembler, MATLAB(R) 9:51
- 02.04.3 grafische Programmierung, Simulink, Datenflussdiagramm 3:33
- 02.04.4 Pseudocode 1:49
- 02.05 imperative Programmiersprachen, Skriptsprachen, dynamische Typisierung 9:26
- 02.06_7 Flussdiagramm, Struktogramm 9:57
!1 - P01 Fotowiderstand mit Servo nachführen 2:26
- 03.01.1 while-, do…while-, for-Schleifen 12:12
- 03.01.2 Schleifen, Sichtbarkeit, break, continue 3:41
- 03.02 Unterprogramme, prozedurale Programmierung 12:32
- 03.03 Code Recycling, API 10:11
- 03.04.1 Funktionen in C, return 11:37
- 03.04.2 Funktionen, void, main 12:24
- 03.04.3 mehrere Parameter, return als GOTO 7:05
- 03.05 Call by Value, statische Variablen 6:01
- 03.06 Deklaration, Definition 3:18
- S03 Temperatursensor des MSP430 0:34
- 03.06a.1 nochmal Funktion, Deklaration, Definition 14:04
!1 - 03.06a.2 nochmal Funktion 3:29
- 04.01 Übersetzung, Compiler, Interpreter 9:29
- 04.02.1 Übersetzung von C und C++ 14:03
- 04.02.2 weiter Übersetzung von C und C++ 4:01
- 04.03.1 Präprozessor, #include, #define 14:50
- 04.03.2 weiter Präprozessor, #include-Guards 14:41
!1!2!3 - 04.04 C-Compiler, Fehler, Warnungen 11:24
- 04.05 Linker, Funktionsnamen 8:07
- 04.06 Sichtbarkeit static, extern 14:23
!1 - 05.01.1 Ganzzahlige Typen, Zweierkomplement 14:11
- 05.01.2 weiter Zweierkomplement 6:11
!1 - 05.02 signed und unsigned char, short, int, long, long long 13:39
- 05.03.1 Überlauf, Teilen durch Null 5:05
- 05.03.2 automatische Umwandlungen bei Ganzzahlen 11:50
!1 - 05.03.3 weiter automatische Umwandlungen bei Ganzzahlen 4:42
!1 - 05.04.1 Festkomma und Gleitkomma 14:00
!1!2 - 05.04.2 float und double 13:01
!1!2 - 05.04.3 keine FPU 4:09
- 05.05.1 eingebaute mathematische Funktionen 11:07
!1!2 - 05.05.2 Division Gleitkomma und Integer, Casting 7:41
!1 - 05.06 Rundungsfehler, Infinity (INF), Not a Number (NaN) 7:53
- P02 Reaktionszeit messen 0:47
- 06.01.1 Arrays 1D, 2D, 3D 10:34
- 06.01.2 weiter Arrays 12:07
- 06.02.1 Arrays initialisieren 10:34
- 06.02.2 Arrays kopieren, memcpy 9:46
- 06.03 Übergabe und Rückgabe von Arrays 12:27
!1 - 06.03a Arrays in Aktion 6:11
- 07.01 Zeichenketten (Strings) 14:56
- 07.02.1 Strings verarbeiten: strlen, strcmp, strcpy 15:25
- 07.02.2 strcat, Strings anhängen 6:19
- 07.03.1 puts, printf, Zeichenketten ausgeben 10:54
!1 - 07.03.2 atoi, sprintf, Umwandlung Zeichenketten, Zahlen 13:02
- 08.01.1 struct, Initialisierung 13:39
!1 - 08.01.2 struct zuweisen, übergeben, vergleichen 11:53
- 08.01.3 Array aus struct 4:53
- 08.02.1 enum, Aufzählungen 13:08
- 08.02.2 switch, weiter enum, Aufzählungen 12:55
!1 - P03 Ein-Knopf-Taschenrechner 0:56
- 09.01.1 Zeiger, Pointer 14:43
!1 - 09.01.2 NULL, ungültige Zeiger 2:49
- 09.02.1 Zeigerarithmetik 10:51
- 09.02.2 weiter Zeigerarithmetik 10:13
- 09.03.1 Dynamischer Speicher, Variable Length Arrays 4:04
- 09.03.2 weiter dynamischer Speicher, malloc, free 14:23
!1!2!3!4 - 09.03.3 weiter dynamischer Speicher, malloc, free 14:28
- 09.03.4 dynamischer Speicher für struct 11:25
- 10.01.1 Präprozessor, Compiler, Linker, include 10:43
- 10.01.2 weiter include, Header 7:01
- 10.01.3 static, extern 11:05
- 10.02.1 grundlegende Typen, char, short, int, long, bool, float, double 7:37
- 10.02.2 Operatoren, Präzedenz 20:35
- 10.02.3 enum, Arrays 10:48
- 10.02.4 Zeichenketten, struct 8:47
- 10.03 if, switch, while, for, Verzweigungen, Schleifen 15:05
- 10.04.1 Funktionen, Deklaration, Definition, return, mathematische Funktionen 15:32
!1 - 10.04.2 Funktionen für Ausgabe, Strings, main 9:45
- P04 Klangausgabe 0:25
!1 - 10.05 Zeiger, NULL, malloc, free 37:26
- 11.01 Theoretische, technische, praktische, angewandte Informatik 11:14
- 11.02 Computer Science, Software Engineering, Information Technology 10:09
- P05 Infrarot-Fernbedienung 1:18
!1 - 12.01.1 Datenstrukturen, Array, Queue, Stack 15:46
- 12.01.2 Baum als Datenstruktur 12:47
!1 - 12.02 Algorithmen 12:27
- 12.02.1 Bubblesort, Quicksort, Laufzeit 29:23
!1 - 12.02.2 Iteration und Rekursion 6:27
!1 - 12.02.3 Komplexität, P und NP 6:46
- 12.02.4 Optimierung, Profiler 5:02
- 13.01 Endliche Automaten 35:16
!1!2 - 13.02.1 Formale Sprachen, Syntaxdiagramm, akzeptierende Automaten 33:41
!1!2 - 13.02.2 HTML, XML, JSON 14:31
!1 - 14.01 Turings Halteproblem 29:29
!1 - 14.02 Code Conventions, Styleguides, ungarische Notation, MISRA 29:02
!1!2!3!4!5!6 - 14.03 defensive Programmierung, assert 18:10
Informatik 1, Winter 2011/2012
16:20:29
- 01A.1 Terabyte und Tebibyte 9:18
- 01A.2 ein Zeichen gleich ein Byte, oder auch nicht 11:31
- 01A.3 Simulator, Debugger, Einzelschritt 14:57
- 01A.4 if-else-Verzweigung 17:55
- 02A.1 Programmablaufplan, Flussdiagramm, Activity Diagram, Maximum bestimmen 27:45
!1!2 - 02A.2 Flussdiagramm, Primzahltest 24:28
!1!2!3!4!5!6 - 03A.1 Programmierbeispiel Teil 1, Top-Down-Entwicklung, MSP430-Projekt einrichten, C-Funktionen 33:10
- 03A.2 Programmierbeispiel Teil 2, Funktionsdefinition, Funktionsdeklaration, Header-Datei 40:40
- 03A.3 Programmierbeispiel Teil 3, Include-Guards, Präprozessor 13:28
- 03A.4 break, continue, return in Schleifen 12:44
- 04A.1 Compiler, Linker; Funktionsweise, Fehler 9:15
- 04A.2 static-Variablen in Funktionen 26:39
- 05A.1 Beispiele Zweierkomplement, Überlauf, signed und unsigned 27:50
- 05A.2 Gleitkommazahlen, float, double, Rundungsfehler, INF, NaN 23:28
- 06A.1 größten Wert in Array bestimmen 9:43
!1 - 06A.2 zweidimensionales Array, stückweise lineare Funktion, lineare Interpolation 23:42
!1 - 07A.1 Suchen und Ersetzen in Zeichenketten in C, Teil 1 1:05:42
!1 - 07A.2 Suchen und Ersetzen in Zeichenketten in C, Teil 2, genaue Grenzen, Off-by-one-Fehler 32:42
- 08A.1 struct und enum am Beispiel Katalog und Warenkorb 38:23
!1 - 08A.2 Kästchenroboter, Teil 1, 2D-Array, struct, enum 57:23
- 08A.3 Kästchenroboter, Teil 2, switch, putchar 49:23
!1!2!3 - 08A.4 Kästchenroboter, Teil 3, Schleifen, struct verwenden 38:16
- 09A.1 Kästchenroboter, Teil 4, malloc, Zeiger wie Arrays 24:59
!1 - 12A.1 Informatik, Datenstrukturen, Array, struct, Warteschlange, Stack, Baum 15:02
- 12A.2 Datenstruktur Sparse Matrix, dünn besetzte Matrix; Implementierung in C; malloc 50:15
!1!2 - 12A.3 Algorithmen, Suchen und Sortieren, Bubble Sort, Quicksort, Laufzeit, O(n log(n)) 1:16:18
!1 - 13A.1 Formale Sprachen, reguläre Ausdrücke, endliche Automaten, Pumping-Lemma 1:06:51
!1!2!3!4 - 13A.2 kontextfreie Sprachen, Syntaxdiagramme für C, Nichtterminalsymbole, Pumping-Lemma 37:25
- 13A.3 Parsen und Auswerten von arithmetischen Ausdrücken, Implementierung 31:36
!1!2!3 - Informatik 1: Praktikumsaufgaben WS 2011/2012 2:19
!1!2 - K01 Überlauf bei Multiplikation 6:18
- K02 if zu switch umwandeln 8:31
- K03 struct und Array verschachtelt 27:15
!1!2 - K04 Gleichheitszeichen in Flussdiagramm und Struktogramm 1:10
- K05 Zeiger und Arrays 24:08
!1
Informatik 1, Winter 2012/2013
18:45:33
- 01B.1 Erste C-Programme, Zuweisung, Einzelschritt-Debugger, while, if 44:24
- S01B Wurzelberechnung in ganzen Zahlen; int, if, while 35:52
!1 - 02B.1 Operatoren, Präzedenz, Short-Circuit-Auswertung 22:08
!1 - 02B.2 Flussdiagramm, Struktogramm, Eingabe in Schleife 24:04
!1 - S02B nächste Zweierpotenz, Schleifen, while, do, for 49:59
- 03B.1 Funktionen in C, Deklaration, Definition; while, do, for 48:03
- S03B.1 Fibonacci-Folge, Rekursion, statische Variablen 28:08
- S03B.2 C-Funktionen entrümpeln 14:31
!1!2 - 04B.1 mehrere C-Dateien, Header-Dateien, #include, Include-Guards 55:26
!1!2 - 04B.2 extern; zwei Verwendungen von static; Linker-Fehlermeldungen 25:36
- 05B.1 bitweise logische Operationen; hexadezimal 11:23
- 05B.2 Beispiele Zweierkomplement; negative Binärzahlen 11:44
!1 - S04B Array; summieren; Maximum bestimmen 41:31
- 07B.1 Arrays und Zeichenketten; strlen 47:17
- S05B.1 Ist Eintrag zweimal in Array 12:12
- S05B.2 Suche in Zeichenkette; UND mit short circuit 24:05
!1!2 - 08B.1 struct für Buch; ISBN-Nummer prüfen 50:24
- S06B struct für Massenpunkte; Schwerpunktsberechnung; Header 36:47
- P1B Zahlenschloss mit Display und Joystick programmieren 22:54
!1 - 09B.1 Fingerübungen zu Zeigern und Arrays 19:28
- 09B.2 Zeiger verwenden, Speicher reservieren 51:20
- S07B Binärzahl aus Zeichenkette in Integer wandeln 19:42
- 10B.1 Morse-Code per Programm; Array von struct 38:48
!1 - S08B Festkommazahlen; Wurzel selbstprogrammiert 41:50
!1!2 - 12B.1 Warteschlange mit Array programmieren 36:29
- S09B Warteschlange mittels struct als Bibliotheksfunktion; Zeiger; malloc 45:12
!1!2!3 - P2B Tic tac toe mit Microcontroller als Gegner 21:40
- 13B.1 Aufzugtür als endlicher Automat in C 35:31
- S10B Datumsberechnungen selbstprogrammiert 29:28
- 14B.1 Programmierfehler finden; Maximum bestimmen 2:56
- 14B.2 Programmierfehler finden; auf Quadratzahl prüfen 6:47
- 14B.3 Programmierfehler finden; auf Zehnerpotenz prüfen 9:30
- 14B.4 Programmierfehler finden; Binomialkoeffizienten berechnen 6:51
- S11B Weg aus Labyrinth programmieren 52:24
!1!2!3!4!5 - P3B Quicksort, Selection Sort, Bubble Sort; Laufzeitkomplexität 1:02:18
- S12B binäre Suche programmieren; Laufzeitkomplexität 38:51
!1!2!3
Informatik 1, Winter 2013/2014
16:39:55
- 01C.1 erste Schritte in C; Beispiele mit while-Schleifen 44:00
- 01C.2 Geltungsbereich von Variablen; Blöcke 6:08
- 01C.3 verschachtelte if-Verzweigungen; ist Wert zwischen Grenzen 20:22
- 01C.4 verschachtelte if-Verzweigungen; kleinsten Wert finden 6:40
!1 - 01C.5 prüfen, ob Zweierpotenz 8:21
!1 - 02C.1 Reihenfolge von plus, mal, geteilt usw. in C 9:34
- 02C.2 Reihenfolge von und, oder, mal, geteilt usw. in C 8:30
- 02C.3 Hexadezimalzahlen; bitweise Operationen 13:05
- 02C.4 stückweise lineare Formel programmieren 8:29
- 02C.5 Teiler zählen; Flussdiagramm; Struktogramm 16:05
!1 - 02C.6 nochmal Hexadezimalzahlen; bitweise Operationen 12:46
- 02C.7 Anwendung von bitweisen Operationen 10:02
- 02C.8 nochmal Reihenfolge von und, oder, mal, geteilt usw. in C 6:38
- 02C.9 drei Bereiche mit if else bilden 3:27
- 02C.10 bitweise Operationen; testen, ob ungerade 9:37
- 03C.1 Quersumme bestimmen; Funktionen in C; for-Schleife 33:10
- 04C.1 kleine C-Funktionsbibliothek schreiben; ganze Zahlen potenzieren 22:11
!1 - 04C.2 Mittelwert einsammeln; statische Variablen in C-Datei 13:42
- 04C.3 Quersumme in beliebigem Zahlensystem; eigene C-Datei mit Header 24:22
- 04C.4 Funktionsbibliothek, die sich Zustand merkt; static 12:39
- 05C.1 Zweierkomplement und Überlauf 25:32
- 05C.2 Formel mit mathematischen Funktionen in C schreiben 7:23
- 05C.3 Gleitkommazahlen, Beispiel mit INF und NaN 5:10
- 05C.4 Beispielrechnungen mit Zweierkomplement 13:30
- 05C.5 mathematische Formel in C schreiben 5:39
- 06C.1 Zahl aufeinanderfolgender großer Werte in Array 34:13
!1!2 - 06C.2 zentrierter gleitender Mittelwert in Array 28:39
!1 - 07C.1 Zeichenkette füllen; Caesar-Verschlüsselung 18:39
!1 - 07C.2 Array von Zeichenketten durchsuchen 21:29
!1 - 07C.3 Inhalt zwischen Tags in Zeichenkette kopieren 10:21
!1 - 08C.1 struct und enum für Telefonbuch 33:38
!1 - 08C.2 struct und enum für Baumdatenbank 36:57
- 09C.1 Beispiele für Adressen, Zeiger, Zeigerarithmetik 21:24
- 09C.2 Arbeit mit Zeigern, Speicherreservierung, malloc 24:06
- 09C.3 Ergebnis mit vorher unbekannter Speichergröße; Punkte innerhalb Rechteck 30:16
!1 - 10C.1 Kreiszahl pi durch Zufallszahlen bestimmen 22:50
- 10C.2 Array am Platz umdrehen 10:47
- 12C.1 eigenen Datentyp Menge implementieren 37:08
!1!2!3!4!5!6!7!8!9 - 12C.2 binäre Suche programmieren 32:49
!1!2 - 12C.3 Zeitkomplexität; Beispiele für Groß-O-Notation 35:02
!1!2 - 12C.4 ähnliche klingende Wörter finden; Soundex-Algorithmus 26:58
- 12C.5 Soundex-Algorithmus mit Speicherreservierung und Header-Datei 54:24
- 12C.6 zweidimensionales Array mit dynamischem Speicher; Spalte einfügen 20:39
- 12C.7 Laufzeitkomplexität O(n), O(log n) usw. 29:29
- 13C.1 Beispiel Syntaxdiagramm, Zustandsdiagramm, endlicher Automat 40:05
!1!2 - 13C.2 Zahlenlisten parsen mittels endlichem Automaten, Teil 1 18:49
- 13C.3 Zahlenlisten parsen mittels endlichem Automaten, Teil 2 26:06
- 14C.1 Beispiele zum Finden von logischen Programmierfehlern 10:35
- P1 Küchentimer mit Embedded Controller 12:11
- P2 Mini-Routenplaner mit Embedded Controller 8:41
- P3 Datumsdifferenz in Tagen mit Embedded Controller 6:38
Informatik 1, Winter 2014/2015
14:05:59
- 01D.1 Bit, Byte, Kilobyte, Beispielrechnungen 3:12
- 01D.2 Variable auf 0 bis 100 eingrenzen 8:03
- 01D.3 von drei Variablen den größen Wert 5:21
- 01D.4 Tarifberechnung mit Rabatt und Limit 6:21
- 01D.5 Summe 1 bis 100; Summe 1²-2²+3²-+…; Fakultät 11:53
- 02D.1 fünf Arten, eine Variable um 2 zu verringern 2:27
- 02D.2 Beispiel für Präzedenzregeln 8:47
!1 - 02D.3 weiteres Beispiel für Präzedenzregeln 6:42
!1 - 02D.4 Hexadezimalzahlen, bitweise Operationen 9:28
!1 - 02D.5 ein einzelnes Bit setzen oder löschen mit bitweisen Operationen 8:32
- 02D.6 Bereich eingrenzen; Flussdiagramm und Struktogramm 4:19
- 02D.7 Fakultät berechnen; Flussdiagramm und Struktogramm 4:10
- 02D.8 auf Zweierpotenz prüfen; Flussdiagramm 3:42
!1 - 02D.9 Präzedenz von Subtraktion und Vorzeichen-Minus, Negation 10:17
- 03D.1 Fakultät mit while-, for- und do…while-Schleife 7:57
- 03D.2 Schleife mit break und continue verändern 9:24
- 03D.3 Primzahlen bis 100 zählen; verschachtelte Schleifen 9:49
- 03D.4 Funktion, die bestimmt, ob eine Zahl zwischen 0 und 100 liegt 11:44
- 03D.5 Funktion, die andere Funktion aufruft; Binomialkoeffizienten ausrechnen 13:43
!1!2!3 - 03D.6 Pseudozufallszahlengenerator mit Werten von 1 bis 6 5:20
- 03D.7 eigener Pseudozufallszahlengenerator; statische Variable 20:41
- 04D.1 Funktion und Variable in eigene Datei auslagern; Header-Datei 27:51
- 04D.2 prüfen, ob Bit gesetzt; Funktion in eigener Datei 13:18
- 04D.3 Fehler in statischer Variable mitzählen 20:44
- 05D.1 Rechnen mit Vorzeichen im Zweierkomplement 13:09
- 05D.2 kleinste und größte Zahl mit 64-Bit-Zweierkomplement 4:46
- 05D.3 Überlauf beim Rechnen mit int-Zahlen 9:40
- 05D.4 Gleitkommazahlen, Lösung einer quadratischen Gleichung 6:13
- 05D.5 Gleitkommzahlen, Zahl der Lösungen einer quadratischen Gleichung 9:48
- 05D.6 Sinus eines in Grad statt Radiant angegeben Winkels 3:53
- 05D.7 komische Effekte durch Rundungsfehler bei Gleitkommazahlen 9:28
- 06D.1 Array mit E6-Reihe füllen 8:46
- 06D.2 Funktion, die den Mittelwert eines Arrays bestimmt 6:33
- 06D.3 Funktion, die mehrfache Einträge aus Array entfernt 10:08
- 06D.4 Sieb des Eratosthenes programmieren 18:31
!1!2 - 07D.1 häufigster Buchstabe in Zeichenkette 17:51
!1 - 07D.2 Buchstaben verwürfeln (Buabhtcbsen vrelüwrefn) 30:46
!1!2 - 07D.3 Zahlen zu ausgeschriebenen Wörtern machen 37:10
- 08D.1 maximaler Abstand vom Ursprung eines Arrays von Punkten 13:24
- 08D.2 Rechteck als struct; Fläche berechnen 6:54
- 08D.3 Schwerpunkt eines Rechtecks mit structs 6:16
!1 - 08D.4 Rechteck aus Material; struct und enum 10:34
- 09D.1 Zeiger auf Strukturen an Funktionen übergeben 19:51
- 09D.2 Beispiele für das Rechnen mit Pointern 15:08
- 09D.3 weitere Beispiele für das Rechnen mit Pointern 6:05
- 09D.4 gleiche Strings in Strukturen finden; Speicherreservierung für Rückgabe eines Arrays 33:07
!1 - 09D.5 weiter gleiche Strings in Strukturen finden; Zeiger auf Zeiger; Laufzeit 39:07
!1!2 - 10D.1 Schleifen, Verzweigungen, Variablen, Zeiger in C 46:45
- 12D.1 einfach verkettete Liste programmieren, Teil 1 41:53
!1!2!3 - 12D.2 einfach verkette Liste programmieren, Teil 2 1:02:55
!1!2!3!4 - 13D.1 Simulation mit wandernden endlichen Automaten, Teil 1 27:07
- 13D.2 Simulation mit wandernden endlichen Automaten, Teil 2 37:35
- 13D.3 Simulation mit wandernden endlichen Automaten, Teil 3, switch, Zeiger 46:17
- K06 statische Variable, Rekursion 2:53
- K07 Binärzahl aus Zeichenkette in Integer wandeln 6:01
- Informatik-Praktikum, Aufgaben WS 2014-2015 3:40
Informatik 2, Sommer 2011
15:59:03
- 01.01 Objektorientierung 24:30
!1 - 01.02.1 C# und .NET 7:32
- 01.02.2 Sprachsynthese, Spracherkennung, Schrifterkennung mit C# 18:15
- 01.03_4 C# Typen, Operationen, Arrays, Klassen, Objekte, public, private 25:04
- 01.05_06 Datenstrukturen, WPF 16:17
!1 - 01.07_08 Datenströme, Exceptions 15:19
- 01.09_10 Multithreading, Netzwerk 14:21
- 01.11_12 Design Patterns, .NET intern 8:43
- S01 C#, WPF, erstes Programm 41:40
!1!2 - 02.01 int, uint, Parse usw. 17:01
- 02.02 Zeichenketten, Strings 9:56
- 02.3.1 Arrays 12:08
- 02.3.2 mehrdimensionale Arrays, rechteckig, jagged 11:56
- 02.4 Aufzählungen, enum 13:43
- P01 Daten aus Dateien plotten 1:11:53
!1 - 03.1 Klassen, Attribute, Methoden 14:38
- 03.2 Überladen von Funktionen bzw. Methoden 7:44
- 03.3 Initialisierung, Konstruktor, Standardkonstruktor 18:53
- 03.4 Getter, Setter, Properties 17:34
- 03.4a Wiederholung Klassen, Attribute, Methoden, Properties 4:53
- 03.5.1 struct, Werttyp, Referenztyp, Teil 1 25:44
!1!2 - 03.5.2 struct, Werttyp, Referenztyp, Teil 2 20:03
- 03.6 statische Attribute, Methoden, Properties 19:37
- 03.6a Wiederholung Klassen, Attribute, Methoden 20:12
- 04.1.1 Datenkapselung, Vererbung, protected 25:12
- 04.1.2 Klassendiagramm in Visual Studio und in UML 12:12
- 04.2 Konstrukturen für abgeleitete Klassen, base 8:37
- 04.3.1 Polymorphie, virtuelle Methoden, Teil 1 14:45
- 04.3.2 virtuelle Methoden und Properties, Teil 2 7:27
- 04.4.1 Polymorphie angewendet, Teil 1 18:31
- 04.4.2 Polymorphie angewendet, Upcast, Downcast, Teil 2 20:02
- 04.5 Zusammenfassung Klassen, Methoden, Vererbung 20:13
- 05.1 abstrakte Klassen, rein virtuelle Methoden 12:53
- 05.2 Interfaces, Mehrfachvererbung 13:10
- 05.3.2 Collections, Lambda-Ausdrücke, anonyme Funktionen 15:29
- 05.3.1 Collections, List, Queue, Dictionary 20:05
- 06.1 Exceptions, Ausnahmebehandlung 19:12
- 06.2 Exceptions, throw, catch, finally 30:11
- 07.0 Dateien, drei Ansätze 8:12
- 07.1.1 Dateien, Verzeichnisse 12:41
- 07.1.2 Rekursion über Verzeichnisse 15:36
- 07.2.1 Datenströme, Streams, Teil 1 12:13
- 07.2.2 Streams, FileStream, BinaryWriter, Teil 2 22:24
- 07.2.3 Streams, StreamReader, Teil 3 7:36
- 07.3 Objektserialisierung 14:22
- 08.1_2 Design Patterns, Singleton-Pattern 10:01
- 08.3 Das Composite-Pattern 15:49
!1 - 08.4 Das State-Pattern 22:29
!1 - 08.5 Das Pattern Model-View-Controller 6:21
- 08.6 Observer-Pattern, Publish and Subscribe, Events 27:25
- 09.1 Multithreading, Multicore, Threads 15:01
- 09.2 Threads, volatile 40:23
- 09.3 Parallele for-Schleife 13:48
- 09.4 Synchronisation von Threads, lock 19:07
!1
Informatik 2, Sommer 2012
16:42:30
- 01B.1 Knöpfe, Radiobuttons, Textfelder mit ein wenig Programmlogik 58:21
- 01B.2 Button, der wegspringt; Zufallszahlen; Schriftarten 43:21
- 02B.1 Arrays; Kleckse nach Abstandsangaben anordnen; Teil 1 50:30
- 02B.2 Kleckse nach Abstandsangaben anordnen; Teil 2 32:12
- 03B.1 eigene Klasse; Vokabeltrainer programmieren; Teil 1 48:02
- 03B.2 Vokabeltrainer programmieren; Teil 2 34:50
- 04B.1 Stausimulation; Klassen, Properties, static; Teil 1 52:23
- 04B.2 Stausimulation; Properties; Minimum und Maximum; Teil 2 50:21
!1 - 05B.1 Schachfiguren; Vererbung, Polymorphie; Teil 1 36:19
!1 - 05B.2 Schachfiguren; Vererbung, Polymorphie; Teil 2 42:06
!1!2!3!4 - 05B.3 Schachfiguren; Bewegung per Maus; Ereignisse; Teil 3 48:12
- 05B.4 Schachfiguren; Hover; weitere Klasse; Refactoring; Teil 4 44:24
!1 - P1B Snake programmieren, ein antikes Videospiel 14:48
- 05B.5 Simulation Amöben und Bakterien; Vererbung, Polymorphie; Teil 1 38:31
!1 - 05B.6 Simulation Amöben und Bakterien; Collections, List; Teil 2 36:24
- 05B.7 Simulation Amöben und Bakterien; Vererbung, Polymorphie; Teil 3 43:17
!1 - 05B.8 Schlüsselwörter von C#; Simulation Amöben und Bakterien; Teil 4 52:43
!1!2!3 - P2B Lastgang simulieren; Polymorphie 7:33
- 06B.1 Beispiel für Exceptions; try, catch, finally, throw 44:28
- 07B.1 Datei mit Stream verarbeiten; Exceptions fangen 45:52
!1 - 07B.2 Text in großer Datei suchen; Streams; Teil 1 35:22
!1 - 07B.3 Text in großer Datei suchen; Streams; Teil 2 44:40
- P3B Schnittpunkte von Freihandlinien markieren 23:14
- 08B.1 Speicherplatznutzung darstellen; Composite-Pattern; Polymorphie 1:14:37
Informatik 2, Sommer 2014
16:03:13
- 01C.1 erste Schritte mit WPF und C#; Tage seit eingegebenem Datum 48:39
!1!2 - 02C.1 eigener Taschenrechner mit WPF 47:58
- 03C.1 persönliches Zeitprotokoll in C#, Teil 1 56:24
- 03C.2 persönliches Zeitprotokoll in C#, Teil 2 54:08
- 03C.3 Intelligenz für Kühlschrank in C#, Teil 1 47:07
!1 - 03C.4 Intelligenz für Kühlschrank in C#, Teil 2 43:51
- 03C.5 Textgenerator mit N-Grammen in C#, Teil 1 43:09
- 03C.6 Textgenerator mit N-Grammen in C#, Teil 2 38:25
!1!2 - 03C.7 Traveling-Salesman-Problem evolutionär lösen, Teil 1 47:21
!1!2 - 03C.8 Traveling-Salesman-Problem evolutionär lösen, Teil 2 38:53
!1 - 04C.1 Fuhrpark in C#, Polymorphie, Teil 1 44:40
- 04C.2 Fuhrpark in C#, Polymorphie, Teil 2 47:52
- 04C.3 Diagramm aus Textdatei in C#, Polymorphie, Teil 1 44:11
- 04C.4 Diagramm aus Textdatei in C#, Polymorphie, Teil 2 38:27
!1!2 - 05C.1 Einteilung Teilnehmer auf Gruppen in C#; Klassen, Collections; Teil 1 48:37
- 05C.2 Einteilung Teilnehmer auf Gruppen in C#; Klassen, Collections; Teil 2 43:42
- 07C.1 Notizzettel auf dem Bildschirm in C#; Fenster erzeugen; Teil 1 39:27
!1 - 07C.2 Notizzettel auf dem Bildschirm in C#; Speichern als XML-Datei; Teil 2 42:38
!1 - 07C.3 perfekte Verschlüsselung, One-Time Pad selbst programmiert 52:25
!1!2 - 08C.1 Differentialgleichungslöser, Strategy-Pattern, Teil 1 33:10
- 08C.2 Differentialgleichungslöser, Strategy-Pattern, Teil 2 26:58
- 08C.3 Differentialgleichungslöser, Mittelpunktsverfahren, Teil 3 35:11
Informatik 2, Sommer 2015
15:06:43
- 01D.1 einfacher Taschenrechner mit C# und WPF 39:22
- 02D.1 Labyrinth erzeugen; rechteckige Arrays; Teil 1 44:12
- 02D.2 Labyrinth erzeugen; Zufall, Arrays, Logik; Teil 2 58:03
!1 - 03D.1 Lastgang simulieren; Objekte in C#; Teil 1 47:57
- 03D.2 Lastgang simulieren; Objekte in C#; Teil 2 38:56
- 03D.3 Lastgang simulieren; Getter, Setter, Properties in C#; Teil 3 43:48
- 03D.4 Lastgang simulieren; Aufrunden, Vererbung; Teil 4 41:49
- 03D.5 struct und class in C#; Werttyp, Referenztyp 16:25
- 04D.1 Zeiterfassung; Vererbung in C#; Teil 1 38:01
- 04D.2 Zeiterfassung; Polymorphie in C#; Teil 2 43:39
- 04D.3 Zeiterfassung, grafische Oberfläche in WPF; Teil 3 37:04
- 04D.4 Zeiterfasssung, virtuelle Methoden, Exceptions; Teil 4 33:50
- 04D.5 Vererbung und Konstruktoren in C#; Zoo 42:27
- 05D.1 Zeiterfassung, Collections, Datei schreiben; Teil 5 41:38
- 05D.2 Gebastel mit Listen, Stacks und Queues 27:05
- 07D.1 Suchen in langer Datei; Streams in .NET; Teil 1 47:13
- 07D.2 Suchen in langer Datei; Streams in .NET; Teil 2 38:02
!1!2 - 07D.3 Suchen in langer Datei; Streams in .NET; Teil 3 45:38
- 08D.1 Bildschirmformular für Wärmedämmung programmieren; Teil 1 39:55
- 08D.2 Bildschirmformular für Wärmedämmung programmieren; Teil 2 31:58
- 09D.1 mit Thread im Hintergrund Primzahlverteilung berechnen 53:59
- 09D.2 Bildeffekt im Hintergrundthread 55:42
Informatik 2, Sommer 2016
11:18:43
- 01E.1 Einstieg in grafische Bedienoberflächen mit WPF 1:10:09
!1 - 02E.1 Schachbrett mit 1, 2, 4, 8 usw. füllen; Arrays, Datentypen; WPF-Elemente per Programm 34:28
!1 - 02E.2 Schiebepuzzle in C# mit WPF; Array; Logik 31:57
!1!2 - 03E.1 Landkarte der Bahnhaltestellen erzeugen; Klassen, Properties, Zeichenfunktionen in C# 1:18:18
- 03E.2 Länge der Luftlinie; struct und static in C# 1:26:00
- 05E.1 Raumschiffspiel in C# mit WPF programmieren, Teil 1 1:06:29
- 05E.2 Raumschiffspiel in C# mit WPF programmieren, Teil 2 44:45
- 05E.3 Raumschiffspiel in C# mit WPF programmieren, Teil 3 58:14
- 06E.1 Bahnfahrplan mit C# und WPF aus dem Netz holen 1:13:51
- 08E.1 Dateien überwachen in C#; Observer-Pattern 1:03:01
!1!2 - 10E.1 Operatoren und Schlüsselwörter von C# 1:11:31
!1!2!3!4
Informatik 2, Sommer 2017
11:05:15
- 01F.1 simpler Taschenrechner mit WPF in C# 1:08:37
- 02F.1 Game of Life mit WPF in C# 1:24:46
- 03F.1 Klassen in C# 1:08:45
- 05F.2 eine 5×5-Determinante ausrechnen 3:56
- 03F.2 Landkarte aus Entfernungstabelle in C# 1:09:53
- 04F.1 Audiosignale mit Klassen und Vererbung in C# 1:01:57
- 04F.2 Ertrag von Windenergieanlagen als Beispiel für Polymorphie in C# 1:19:49
- 05F.1 class, abstract class, interface, struct in der Sprache C# 7.0 30:07
- 05F.2 Arbeit mit generischen Collections in C# 35:58
- 07F.1 Dateien und Streams in .NET, Teil 1: File und Stream 41:13
- 07F.2 Dateien und Streams in .NET, Teil 2: BinaryWriter und StreamWriter 15:54
- 07F.3 Dateien und Streams in .NET, Teil 3: Exceptions und using 28:13
- 09F.1 Webcrawler in C# mit Regular Expressions und Threads 1:16:07
Mathe 1 Teil 1, Winter 2010/2011
33:16:07
- 01.01.1 drei Arten Mathematik 6:22
- 01.01.2 weiter drei Arten Mathematik 2:05
- 01.02.1 Modell und Wirklichkeit 6:19
- 01.02.2 weiter Modell und Wirklichkeit 7:19
- 01.03.1 dieses Semester, Numerik 3:05
- 01.03.2 Logik und Mengen 7:58
- 01.03.3 Zahlen 5:28
- 01.03.4 Kombinatorik 3:06
- 01.03.5 Abbildungen und Funktionen 2:37
- 01.03.6 Vektorrechnung 4:00
- 01.03.7_8 Ableitung, Integral, Zufall 6:14
- 01.04 Software 4:42
- 01.05.1 Rechnen mit Pfeilen 5:14
- 01.05.2 von Pfeilen zu Vektoren 6:19
- 01.06.0.1 Vektoren in Zahlen 10:04
- 01.06.0.2 weiter Vektoren in Zahlen 3:07
- 01.06.1 Skalarprodukt 5:17
- 01.06.2.1 Vektorprodukt 8:37
!1 - 01.06.2.2 weiter Vektorprodukt 10:20
- 02.01.1 Momentangeschwindigkeit, Ableitung 8:17
- 02.01.2 Ableitung 11:03
- 02.01.3.1 Ableitungsregeln 6:03
- 02.01.3.2 Einschub Schreibweise Ableitung 3:24
- 02.01.3.3 Kettenregel, Ableitung Exponentialfunktionen, Logarithmus 8:36
- 02.01.3.4 Ableitung Potenzen, Wurzeln, Sinus 10:00
- 02.01.3.5 weiter Ableitung Sinus 6:27
- 02.02.1.1 Integral, Stammfunktion 10:35
- 02.02.1.2 weiter Stammfunktionen 3:02
- 02.02.1.3 weiter Stammfunktionen 3:11
- 02.02.2.1 bestimmtes Integral 9:25
- 02.02.2.2 weiter bestimmtes Integral 7:11
- 03.01 Naive Mengenlehre 4:46
!1 - 03.02 Mengenoperationen, Mengenrelationen 7:21
- 03.03.1 Aussagen, Prädikate, logische Operatoren 6:26
- 03.03.2 weiter Aussagen, Prädikate, logische Operatoren 9:34
!1 - 03.03.3 weiter Aussagen, Prädikate, logische Operatoren 6:47
- 03.04.1 Logische Folge 7:53
- 03.04.2 Logische Äquivalenz 3:45
- 03.05.1 Rechenregeln für Mengen und Logik, De-Morgan-Gesetze 10:53
- 03.05.2 Rechenregeln, Wahrheitstabelle 5:19
- 03.06.1 Mengenbildung durch Auswahl; Kreisscheibe 10:29
- 03.06.2 axiomatische Mengenlehre 6:39
- 04.01 Natürliche, ganze und rationale Zahlen 3:34
- 04.02 Reelle Zahlen 4:54
- 04.03.1 Komplexe Zahlen 6:49
- 04.03.2 Real- und Imaginärteil, Länge, Gaußsche Zahlenebene 6:52
- 04.03.3 Wozu komplexe Zahlen? 5:31
- 04.04 Rechenregeln, Assoziativität, Kommutativität, Distributivität 6:15
- 04.05 Quaternionen, unendlich große Zahlen 4:16
- 04.06 Intervalle reeller Zahlen 2:42
- 04.07 Stellenwertsysteme, Binärsystem 8:51
- 04.08 Exponentialschreibweise 5:50
- 05.01 Äquivalenzumformung, Lösungsmenge 3:46
- 05.02.1 Monoton steigende Funktionen 9:50
- 05.02.2 Monoton fallende Funktionen 8:00
- 05.03 quadratische Ungleichungen 6:01
- 05.04 Polynom-Ungleichungen 13:01
- 05.05.1 Bruch-Ungleichungen mit 0 5:22
- 05.05.2 Bruch-Ungleichungen 2:44
- 05.06 Betragsungleichungen 3:15
- 05.07 Gemischte Ungleichungen 3:41
- 06.01 Begriff Kombinatorik, Potenzmenge 9:27
- 06.02 Variation mit Wiederholung 9:31
- 06.03 Variation ohne Wiederholung, Permutation, Fakultät 9:29
- 06.04.1 Kombination ohne Wiederholung, Binomialkoeffizient 10:22
- 06.04.2 Kombination ohne Wiederholung, Binomialkoeffizient 5:33
- 06.05 Rechenregeln für Binomialkoeffizienten 8:26
- 06.06.1 Wiederholung Kombinatorik, allgemeine binomische Formel 12:44
- 06.06.2 weiter allgemeine binomische Formel 8:45
- 07.01.1 Begriff Funktion, Abbildung 11:14
- 07.01.2 weiter Begriff Funktion, Abbildung 7:09
- 07.02.1 Funktionen als Maschinen, Tabellen, Pfeildiagramme 10:58
- 07.02.2 Funktionen als Kurven 10:02
- 07.03 Funktionen in der Mathematik und beim Programmieren 7:24
- 07.04.1 Bildmenge, Wertebereich einer Abbildung 7:09
- 07.04.2 weiter Bildmenge 10:01
- 07.04.3 weiter Bildmenge, Einheitskreis 11:06
- 07.04.4 weiter Bildmenge, logarithmische Spirale 6:41
!1 - 08.01 Kartesisches Produkt, R2, R3 7:51
!1 - 08.02 Geordnete Tupel, Arrays, Strukturen 10:59
- 08.03 Begriff Relation 5:58
- 08.04.1 Relationen als Tabellen 13:59
- 08.04.2 Relationen als Diagramme und als geometrische Objekte 14:32
- 08.05 Idee der Umkehrabbildung, Umkehrfunktion 7:59
- 08.06.1 Definition der Umkehrbarkeit 10:35
- 08.06.2 Potenzen von Funktionen, Identität 4:57
!1 - 08.06.3 Umkehrfunktionen und Funktion verkettet 2:58
- 08.07 Kriterien Umkehrbarkeit 13:35
- 08.08.1 Beispiele Umkehrbarkeit 4:10
- 08.08.2 weiter Beispiele Umkehrbarkeit 13:21
- 08.08.3 weiter Beispiele Umkehrbarkeit 6:34
- 09.01 monotone, gerade, ungerade, periodische Funktionen 13:02
- 09.02.1 Lineare Funktionen, Achsenabschnittsform 8:57
- 09.02.2 weiter lineare Funktionen, Steigung, Achsenabschnitt 4:14
- 09.03 Potenzfunktionen 11:08
- 09.04 Wurzelfunktionen 9:24
- 09.05 Rechenregeln für Potenzen und Wurzeln 14:22
- 10.01 Exponentialfunktionen 10:00
- 10.02.1 Eulersche Zahl, Exponentialfunktion 12:49
- 10.02.2 weiter Eulersche Zahl, Exponentialfunktion 14:10
!1!2 - 10.03.1 Beispiele Wachstum, Zerfall, Skalen 10:38
!1 - 10.03.2 Beispiele Boltzmann-Statistik, Diodenkennlinie 14:06
- 10.04 Logarithmen 10:04
- 10.05 Rechenregeln für Logarithmen 10:14
- 10.06 Beispiele Logarithmus; Dezibel, Oktaven, Bits 6:54
- 10.07 halblogarithmisches, doppeltlogarithmisches Diagramm 13:05
- 11.01 Polynome, Begriffe, Verlauf 8:39
- 11.02 Polynome angewendet, Näherung, Interpolation, Differentialgleichung 14:58
!1!2 - 11.03 Polynomdivision 9:18
!1!2 - 11.04.1 Nullstellen und Linearfaktoren 10:01
- 11.04.2 weiter Nullstellen und Linearfaktoren 6:20
- 11.05 Horner-Schema 3:18
- 12.01 Algebraische Gleichungen 8:19
- 12.02 Satz von Vieta 8:17
- 12.03 Quadratische Gleichung 14:34
- 12.04_5 kubische Gleichungen und Gleichungen höheren Grades 11:23
- 12.06.1 Nullstellensuche, Newton-Verfahren 8:45
- 12.06.2 weiter Newton-Verfahren 13:35
- 12.06.3 weiter Newton-Verfahren 9:45
- 13.01 Rationale Funktionen 3:42
- 13.02.1 z-Transformation 14:36
- 13.02.2 weiter z-Transformation, Rückkopplung 12:49
- 13.03.1 Nullstellen und Pole 12:22
!1!2 - 13.03.2 weiter Nullstellen und Pole 4:40
- 13.04 Asymptoten 7:13
- 14.01 Faktorisierung von Polynomen, Partialbruchzerlegung 8:02
- 14.02 Partialbrüche für ganze Zahlen 12:23
!1 - 14.03 Partialbruch, einfache Polstelle 12:26
- 14.04 Partialbruch, mehrfache Polstelle 10:33
- 14.05 Partialbruch, quadratischer Term 11:58
- 14.06 Partialbrüche allgemein 7:19
- 14.07 Konstanten der Partialbrüche bestimmen 10:57
!1!2!3!4!5!6 - 15.00 Verkettung von Funktionen 14:39
- 15.01 Vertikale Verschiebung und Streckung von Funktionsgraphen 8:14
- 15.02.1 Horizontale Verschiebung und Streckung von Funktionsgraphen 7:23
- 15.02.2 weiter Horizontale Verschiebung und Streckung von Funktionsgraphen 8:22
- 16.01 Rechtwinkliges Dreieck, Hypotenuse, Kathete, Pythagoras 5:52
- 16.02 Sinus, Cosinus, Tangens, Cotangens 14:01
- 16.03 Bogenmaß, Gon 7:46
- 16.04 Sinus, Cosinus, Tangens am Einheitskreis 8:03
- 16.05 Sinussatz 8:10
- 16.06 Cosinussatz 12:13
- 16.07.1 arcsin, Arcussinus 9:21
!1!2 - 16.07.2 arccos, arctan, Arcuscosinus, Arcustangens 14:58
- 16.07.3 atan2, Arcustangens 2:46
- 17.01 Gaußsche Zahlenebene, komplexe Zahlen 10:40
- 17.02 Betrag, Winkel einer komplexen Zahl 12:44
- 17.03 Addition, Subtraktion komplexer Zahlen 4:32
!1 - 17.04 Multiplikation komplexer Zahlen 14:47
- 17.05.1 Division komplexer Zahlen 13:02
- 17.05.2 weiter Division komplexer Zahlen, Winkel bestimmen 2:36
- 18.01.1 Ganzzahlige Potenzen und Wurzeln komplexer Zahlen 13:53
- 18.01.2 Wurzeln in Wolfram Alpha 1:46
- 18.01.3 weiter Wurzeln komplexer Zahlen 4:17
- 18.02.1 Eulersche Identität e^(ix)=cos(x)+isin(x) 11:42
- 18.02.2 weiter Eulersche Identität 12:51
- 18.03 sin, cos, Potenzreihen, Additionstheoreme 14:19
- 18.04.1 Polardarstellung, Multiplikation, Division, Potenz 8:00
- 18.04.2 weiter Polardarstellung, Wurzel 7:39
- 18.05.1 Fundamentalsatz der Algebra, komplexe Nullstellen 14:50
!1!2 - 18.05.2 weiter Fundamentalsatz der Algebra, komplexe Nullstellen 14:31
!1!2!3 - 19.01 Folgen 14:33
- 19.02 beschränkte, monotone Folgen 5:43
- 19.03.1 Konvergenz, bestimmte Divergenz 18:42
- 19.03.2 weiter Konvergenz, Grenzwert 11:30
- 19.04 Grenzwertsätze 11:35
- 19.05 Grenzwerte von Funktionen 15:30
!1 - 19.06 Stetigkeit, stetig hebbare Definitionslücken 24:33
- 19.07 Regel von L’Hôpital, Null durch Null 14:11
!1!2 - 20.01 Ableitung, Tangente, Sekantensteigung 27:11
- 20.02 Ableitung von Summen und Produkten 11:26
- 20.03 Kettenregel 19:44
!1!2 - 20.04 Quotientenregel 6:44
- 20.05_6_7 Ableitung exp, log, Potenz 13:25
- 20.08 Ableitung sin, cos, arcsin 11:28
- 21.01 lokale, globale Minima, Maxima 15:59
!1 - 21.02 lokale Minima und Maxima, Kriterien 14:27
- 21.03 Wendepunkte 11:11
- 22.01 Lineare Näherung und ihr Fehler 29:52
!1!2 - 22.02 Numerische Schätzung 1., 2. Ableitung 14:10
- 23.01 Idee des Integrals 22:41
!1 - 23.02 Stammfunktion, unbestimmtes Integral, Hauptsatz 21:02
- 23.03 Uneigentliche Integrale 15:43
- 23.04 Numerische Integration, Trapezregel, Simpson-Regel 19:50
- 24.01 Partielle Integration 17:23
- 24.02 Substitutionsregel 13:23
- 24.03 Integration durch Partialbruchzerlegung 21:00
- 25.01.1 Kreisfläche, Volumen von Zylinder, Prisma, Kegel, Pyramide 20:43
- 25.01.2 Kugelvolumen, Kugelfläche 17:47
- 25.02 Bogenlänge 15:45
!1!2!3 - 25.03 Volumen von Rotationskörpern 18:01
- 25.04 Oberfläche von Rotationskörpern 21:23
- 26.01 Wahrscheinlichkeit, Ereignisse 21:25
- 26.02 Wahrscheinlichkeitsbegriffe, Häufigkeit, Bayes, Laplace 10:56
!1 - 26.03 Kolmogorow-Axiome der Wahrscheinlichkeit 23:23
!1 - 27.01_02 Zufallsvariablen, Erwartungswert einer diskreten Zufallsvariable 18:23
- 27.03 Stetige Zufallsvariable, Wahrscheinlichkeitsdichte 23:08
!1 - 27.04 Erwartungswert für stetige Zufallsvariablen 5:17
!1 - 27.05 Median, Perzentilen 13:31
- weiter gehts in der nächsten Playliste 0:11
Mathe 1 Teil 2, Winter 2010/2011
2:17:24
- 28.01 Varianz, Standardabweichung 13:37
- 28.02 Varianz, Standardabweichung berechnen 13:13
- 28.03 Normalverteilung, zentraler Grenzwertsatz 14:59
- 29.01_02 Statistik, Stichprobe, Grundgesamtheit, Schätzung des Erwartungswerts 26:37
- 29.03 Schätzung der Varianz 26:58
!1 - A01.1 Korrelationskoeffizient, Regressionsgerade 7:01
- A01.2 Korrelation 8:52
- A01.3 Achsenabschnitt der Regressionsgerade 7:50
- A01.4 Steigung der Regressionsgerade 7:43
!1 - A01.5 Fehler der Regressionsgeraden, Pearson-Korrelationskoeffizient 10:34
Mathe 1, Winter 2011/2012
26:34:04
- 01A.1 Skalarprodukt und Vektorprodukt 16:11
- 02A.1 Kehrwert ableiten 14:32
- 02A.2 Wurzel ableiten 14:54
- 02A.3 Faktor-, Summen- und Produktregel der Ableitung 14:04
- 02A.4 Quotientenregel 7:39
- 02A.5 Kettenregel 10:34
- 02A.6 kompliziertere Ableitung 4:28
- 02A.7 Ableitung und Wurfparabel 18:05
- 03A.1 Mengenoperationen, logische Operationen, Mengendifferenz, Exklusiv-Oder 20:02
- 03A.2 komplexe geometrische Mengen, Rechteck und Kreisscheibe als Menge, Kreisformel 21:22
- 04A.1 Ordinalzahlen, Konstruktion von Zahlen nur aus der leeren Menge 13:32
!1 - 04A.2 Mächtigkeit, 1. und 2. Cantorsches Diagonalverfahren, (Über-)Abzählbarkeit 25:46
- 04A.3 Beispiel für Multiplikation und Division komplexer Zahlen 8:44
- 04A.4 Warum i² gleich -1 sein muss 13:37
!1 - 05A.1 Bruch-Ungleichung, Beispiel 13:50
- 06A.1 Kombinatorik, Fakultät, Binomialkoeffizient 10:52
- 06A.2 Kombinatorik, Telefonnummern abzählen 3:59
- 06A.3 Kombinatorik, Passwort aus bekannten Buchstaben 8:35
- 06A.4 Kombinatorik, Zahl ohne doppelte Ziffern 2:26
- 06A.5 Kombinatorik, mehre Münzen, Binomialverteilung 19:50
- 06A.6 Kombinatorik, vier Richtige im Lotto, hypergeometrische Verteilung 7:44
- 07A.1 Bild einer quadratischen Funktion, Umkehrbarkeit 14:01
- 09A.1 Gerade und Exponentialfunktion durch zwei Punkte, beschränkt, monoton, umkehrbar 16:46
- 10A.1 Fakultät schätzen, Stirlingformel, Potenzgesetze und Logarithmengesetze anwenden 24:44
- 10A.2 Beispiele zu Potenz- und Logarithmusgesetzen 19:25
- 10A.3 Zinseszins, Exponentialfunktion schätzen, Definition der Eulerschen Zahl 13:01
!1 - 10A.4 radioaktiver Zerfall, Halbwertszeit, Exponentialfunktion schätzen, Logarithmengesetze 7:36
!1 - 10A.5 Poisson-Verteilung hergeleitet mit Binomialkoeffizient, Exponentialfunktion 21:09
- 11A.1 Parabel durch drei Punkte 13:46
- 11A.2 geometrische Reihe, Polynomdivision, Periode 9 26:41
- 13A.1 rationale Funktion mit gegebener Asymptote, Nullstelle, Polstelle 18:56
!1 - 14A.1 Partialbruchzerlegung, Pole, Bestimmung der Konstanten, Integral einer rationalen Funktion 55:48
!1!2!3 - 14A.2 Beispiel Partialbruchzerlegung 5:08
!1 - 15A.1 Funktionsgraphen strecken, stauchen, verschieben; Verkettung von Funktionen 30:51
!1 - 15A.2 Achsen skalieren, verschieben; sinusförmige Welle, Amplitude, Frequenz, Anfangsphase 26:32
- 16A.1 Sinus hyperbolicus, sinh, cosh, Areafunktionen 49:20
!1 - 16A.2 Cosinus vom Arcuscosinus und umgekehrt, Mehrdeutigkeiten bei den Winkelfunktionen 18:41
!1 - 17A.1 Fingerübungen mit komplexen Zahlen, Länge, Winkel; Potenzen; Wurzeln von i 13:39
!1!2 - 17A.2 Die Werte von 1 durch (3+ix) bilden einen Kreis in der Gaußschen Zahlenebene 16:10
- 18A.1 Eulersche Identität, Polardarstellung, Sinus hyperbolicus 36:09
- 18A.2 Multiplikation am Einheitskreis geometrisch, Länge, komplex Konjugiertes 26:35
- 18A.3 Gleichungen und pq-Formel mit komplexen Zahlen 11:10
- 18A.4 Zwei hoch die imaginäre Einheit i; imaginäre Einheit hoch die imaginäre Einheit 12:08
- 19A.1 Grenzwertbestimmung für komplizierte Funktion, Grenzwertsätze, Stetigkeit 14:02
- 19A.2 Beispiel für Regel von L’Hôpital 5:07
- 19A.3 null hoch null als Grenzwert; Stetigkeit 12:57
- 20A.1 Fingerübungen zu Ableitungen; Kettenregel, Potenzregel, Produktregel, Quotientenregel 11:59
!1 - 20A.2 Schätzen mit der Ableitung; Tangentengerade 18:59
- 20A.3 Nur bei Exponentialfunktionen ist die Ableitung konstantes Vielfaches der Funktion 8:33
- 20A.4 Ableitung Tangens und Arkustangens 20:18
- 21A.1 Beispiel lokales Maximum, lokales Minimum 12:59
- 21A.2 Ableitung größer null, streng monoton 7:30
- 21A.3 optimale Dose, maximales Volumen, minimale Oberfläche, Ableitung 35:52
- 21A.4 schnellste Verbindung, Ableitung, snelliussches Brechungsgesetz der Optik 14:32
!1!2!3 - 22A.1 Ableitung von Messreihen schätzen, numerisches Differenzieren, Fehlerschätzung 30:00
!1!2!3 - 23A.1 Zusammenfassung bestimmtes Integral, Stammfunktion, Wurzelfunktion integrieren 11:51
!1!2 - 23A.2 Pi mit Integral und Arcustangens berechnen; Leibniz-Reihe 13:08
- 23A.3 numerische Integration, Trapezverfahren, Fehlerschätzung, Romberg, Richardson 22:41
!1 - 24A.1 Partielle Integration, Substitutionsregel, Integration durch Partialbruchzerlegung 19:33
!1!2 - 24A.2 Beispiele partielle Integration, Substitutionsregel, Integration durch Partialbruchzerlegung 37:16
!1!2 - 25A.1 Kreisfläche, Kugelvolumen, Kugeloberfläche 15:47
- 25A.2 Bogenlänge, Kettenlinie, Cosinus hyperbolicus, cosh 20:58
- 25A.3 Rotationskörper, Volumen, Mantelfläche, Kugelvolumen, Kugelfläche 16:26
!1!2!3!4 - 25A.4 Schwerpunkt eines Flächenstücks mittels Integral 29:06
!1!2!3 - 26A.1 Wahrscheinlichkeit, Kolmogorow, Ereignis, unvereinbar, unabhängig 35:47
!1 - 26A.2 Beispiel Binomialverteilung, Beispiel Laplace-Experiment 23:59
!1 - 27A.1 diskrete Zufallsgröße, Histogramm, Binomialverteilung, Poisson-Verteilung, Erwartungswert 47:22
!1 - 27A.2 Roulette, Erwartungswert 10:00
- 27A.3 diskrete vs. stetige Zufallsgröße, Wahrscheinlichkeitsdichte 34:25
- 27A.4 Erwartungswert und Median einer stetigen Zufallsgröße 10:36
- 28A.1 Varianz, Standardabweichung einer Zufallsgröße 36:55
- 28A.2 Mittelwertbildung verringert Varianz und Standardabweichung 21:30
!1 - 28A.3 Normalverteilung, zentraler Grenzwertsatz, Skizze einer Herleitung 1:07:20
!1!2 - 28A.4 Normalverteilung in OpenOffice.org, Wahrscheinlichkeitsdichte, kumulierte Verteilungsfunktion 27:16
- 29A.1 Schätzung Mittel, Varianz, Standardabweichung; Stichprobe; OpenOffice.org; robuste Statistik 29:18
- K01 Ungleichung 14:59
- K02 Gleichung mit komplexen Zahlen 9:35
- K03 Grenzwert n gegen unendlich 8:02
- K04 Kombinatorik, Trinom ausmultiplizieren 3:43
- K05 Bogenlänge 9:13
- K06 Gleichung mit Logarithmus, Wurzel, Potenz 4:08
- K07 rationale Funktion, Polstellen, Asymptote, Partialbruchzerlegung 12:45
- K08 kubische Parabel, Zahl der Nullstellen 13:12
- K09 Integral x durch Wurzel 1 plus x², partielle Integration, Substitutionsregel 6:51
- K10 Funktionsgraph verschieben, umformen 5:15
- K11 Ableitung, Kettenregel 2:04
- K12 Längen im Dreieck bestimmen, Cosinussatz, Sinussatz 10:25
- K13 quadratische Gleichung mit komplexen Zahlen 7:40
- K14 Torus, Volumen, Rotationskörper 13:08
!1!2!3!4!5!6!7!8
Mathe 1, Winter 2012/2013
32:20:08
- 01B.1 Formales zur Mathe-Veranstaltung; Videos, Skripte, Inverted Classroom 22:30
!1!2 - 01B.2 Geraden in 3D auf Parallelität prüfen 19:30
- 01B.3 Schnittpunkt zweier Geraden in 3D, Geradengleichung 8:14
- 01B.4 Geradengleichung in 2D, Vektorgleichungen umformen 12:41
- 01B.5 Abstand einer Gerade vom Ursprung, senkrechte Vektoren, Skalarprodukt 27:51
- 01B.6 Vektorprodukt, senkrecht, Rechte-Hand-Regeln, Drehbewegung 11:57
- 02B.1 Abstand zweier windschiefer Geraden per Ableitungen 29:07
!1 - 02B.2 Quotientenregel, Kettenregel angewendet 6:35
- 02B.3 Wurzel(52) schätzen, Tangentengerade an Wurzelfunktion 21:32
- 02B.4 Fläche unter Sinus-Halbwelle 5:19
- 02B.5 Strecke aus Geschwindigkeitsverlauf, Integral, Stammfunktion, Einheiten 29:13
- 02B.6 Fläche unter Parabel halbieren, Integral 18:33
- 02B.7 Schwerpunkt der Fläche unter Parabel, Integral 16:05
- 03B.1 geometrische Mengen, Prädikate, Schnitt und Vereinigung 13:56
- 03B.2 logische Folge und Äquivalenz, Beispiele 7:34
- 03B.3 Exklusiv-Oder mit Und, Oder, Nicht ausdrücken 10:58
- 04B.1 Rechnen mit komplexen Zahlen, Multiplikation und Division 11:28
- 04B.2 Wurzel aus der imaginären Einheit 19:19
- 04B.3 quadratische Gleichung mit komplexwertigen Lösungen 4:23
- 04B.4 rationale Zahlen, periodische Dezimalbrüche, algebraische Gleichungen 16:34
- 05B.1 Zahlenintervalle vereinen, schneiden 5:39
- 05B.2 Ungleichung mit Betrag und Quadrat 36:53
- 05B.3 Ungleichungen mit Produkt von Linearfaktoren 16:27
!1 - 05B.4 Ungleichung mit Quadrat im Betrag 21:58
!1 - 05B.5 Ungleichung mit Bruch 15:03
- 06B.1 mögliche Telefonnummern abzählen 6:19
- 06B.2 (a+b+c)^42 ausmultiplizieren, Binomial- und Trinomialkoeffizienten 18:08
- 06B.3 Farbmuster abzählen 8:44
- 06B.4 Passwort mit fünf Zeichen, eines doppelt 4:23
- 06B.5 fünfstellige Zahl, nur viermal Ziffer wiederholen 4:25
- 06B.6 (1+x durch 10)^10 mit Binomialkoeffizienten 13:16
- 06B.7 Passwort mit einem Großbuchstaben und einer Ziffer 2:54
!1 - 07B.1 Funktion, Abbildung, Rechenvorschrift, Graph, Definitionsmenge 19:55
- 07B.2 sin(1 durch x), Graph, Bildmenge 12:06
- 07B.3 x + 1 durch x, Graph, Bildmenge 9:33
- 07B.4 rekursive Funktionsdefinition, Fibonacci-Folge 9:52
- 07B.5 Kardioide; Kurve versus Funktionsgraph 29:53
- 07B.6 e hoch x³, Bildmenge, Graph, Unterschied f und f(x) 17:07
- 08B.1 dritte Wurzel von e^(5x) + 2 auflösen, Umkehrfunktion 21:49
- 08B.2 Funktion, Umkehrfunktion, Potenzen von Funktionen 3:19
- 09B.1 Beispiele für monoton wachsende und fallende Funktionen; Potenzrechengesetze 11:43
- 09B.2 Beispiele für (nicht)periodische Funktionen 8:13
- 09B.3 Beispiele für gerade und ungerade Funktionen 6:52
- 10B.1 Wurzel und Potenz auflösen 3:49
- 10B.2 Logarithmus und Potenz auflösen 10:25
- 10B.3 Richter-Skala; Dezibel; logarithmische Größen 22:24
!1!2!3 - 10B.4 Logarithmus einer Summe 11:30
- 10B.5 Logarithmus eines Quadrats 10:42
- 10B.6 Potenzfunktion im doppeltlogarithmischen Diagramm 11:01
- 11B.1 Polynom 4. Grades; Nullstellen; biquadratische Gleichung; Näherung an Cosinus 12:42
- 11B.2 ganzzahlige Nullstellen; Satz von Vieta; Polynom 3. Grads 6:54
!1 - 11B.3 Polynomdivision, Beispiel 10:37
!1 - 11B.4 Polynom aus Steckbrief; Achsenberührung 14:07
- 11B.5 kubische Parabel; Kriterium für Höcker 6:12
- 11B.6 Polynom in Linearfaktoren zerlegen 9:22
- 11B.7 Polynom in Linearfaktoren und Faktor ohne Nullstellen zerlegen 14:13
- 11B.8 Verlauf einer kubischen Parabel 6:36
- 12B.1 Newton-Verfahren; Schnittpunkte Cosinus und Normalparabel 8:05
- 12B.2 Newton-Verfahren; Wurzel 5 mit Grundrechenarten; Konvergenzgeschwindigkeit 33:22
!1 - 12B.3 Newton-Verfahren für x^x = cos(x); Ableitung von x^x 5:42
!1 - 13B.1 rationale Funktion vereinfachen; Nullstellen, Polstellen, Asymptoten 11:54
- 13B.2 rationale Funktion; Nullstellen, Polstellen, Asymptoten 8:44
- 13B.3 rationale Funktion; Nullstellen, Polstellen, stetig hebbare Definitionslücken 11:28
- 13B.4 rationale Funktion; Asymptote; Polynomdivision 2:49
- 13B.5 rationale Funktion; Asymptote; Polynomdivision; Asymptotenpolynom 9:14
- 13B.6 rationale Funktion; Asymptote gegeben, Nennerpolynom finden 6:31
- 13B.7 rationale Funktion nach Steckbrief; Polstelle, Nullstelle, Asymptote 9:40
!1 - 13B.8 rationale Funktion skizzieren an Nullstellen, Polstellen 4:01
- 14B.1 Beispiel für Partialbruchzerlegung 23:49
!1 - 14B.2 Wozu Partialbruchzerlegung; Herleitung Partialbruchzerlegung 13:57
- 14B.3 Beispiel für Partialbruchzerlegung; Polynomdivision 6:51
!1 - 14B.4 rationale Funktion; Nullstellen, Polstellen, Partialbruchzerlegung, Integral 35:40
!1 - 15B.1 Graph der Wurzelfunktion verschieben, strecken, stauchen 18:55
- 15B.2 sinusförmige Schwingung; Amplitude, Phase; Graph verschieben, strecken, stauchen 12:11
- 15B.3 Sinus vom Betrag mit Verschiebung 3:21
- 15B.4 Funktion mit Betrag verschieben 19:01
- 15B.5 Sinus ins Quadrat skizzieren 2:58
- 16B.1 Sinus, Cosinus, Tangens; Sinussatz, Cosinussatz 10:00
- 16B.2 Dreiecksberechnung, zwei Seiten und ein Winkel gegeben 7:46
- 16B.3 Dreiecksberechnung, drei Seiten gegeben 5:38
- 16B.4 Dreiecksberechnung, Fläche aus drei Seitenlängen 14:53
- 16B.5 Dreiecksberechnung, zwei Seiten und ein Winkel gegeben (andere Situation) 6:37
- 16B.6 Dreiecksberechnung, Seitenhalbierende 14:15
!1 - 16B.7 Dreiecksberechnung, Winkelhalbierende 7:29
!1!2 - 17B.1 Multiplikation komplexer Zahlen algebraisch und geometrisch 15:52
- 17B.2 Division komplexer Zahlen algebraisch und geometrisch 18:38
- 18B.1 dritte Wurzeln einer komplexen Zahl 14:17
- 18B.2 Gleichung mit komplexen Zahlen; Wurzel aus i 4:52
- 18B.3 quadratische Gleichung mit komplexen Zahlen 3:06
- 18B.4 Drehungen im R2 über komplexe Zahlen und Eulersche Identität 9:30
- 18B.5 Cosinus von i; Cosinus mit e hoch i phi schreiben 12:13
- 18B.6 Logarithmus einer komplexen Zahl 9:43
- 18B.7 komplexe Linearfaktoren eines Polynoms 6:19
- 19B.1 Grenzwertbetrachtung mit Bruch und Potenzen 6:01
- 19B.2 Grenzwertbetrachtung mit Bruch und Wurzel 9:07
- 19B.3 Grenzwertbetrachtung mit Bruch und Wurzel, anderes Beispiel 7:23
- 19B.4 Grenzwertbetrachtung mit Bruch und Cosinus 2:21
- 19B.5 Grenzwertbetrachtung mit Sinus, Bruch und Potenzen 1:45
- 19B.6 Grenzwertbetrachtung; L’Hospital 5:25
- 19B.7 Exponentialfunktion wächst schneller als jedes Polynom 5:40
- 19B.8 Logarithmus wächst langsamer als jede Wurzel 5:13
- 19B.9 Grenzwert n-te Wurzel aus n 4:38
- 19B.10 Grenzwertbetrachtung rationale Funktion; L’Hospital 2:35
- 19B.11 erfundene Regeln und ein zu knapper Beweis 11:26
- 20B.1 Ableitungen, ein paar Fingerübungen 22:36
- 20B.2 zentrale Differenzformeln; Ableitung numerisch 8:12
- 20B.3 senkrechter Wurf; Differentialgleichung 23:42
- 20B.4 Kondensator entladen; Differentialgleichung 14:12
- 21B.1 Minimum, Maximum eines Polynoms 8:21
- 21B.2 Monotonie mit Ableitung nachweisen 5:01
- 21B.3 Monotonie und Ableitung, Problemfall 5:08
- 21B.4 Wendepunkte Glockenkurve 10:39
!1!2 - 21B.5 Polynom mit vorgegebenen Wendepunkten 12:57
!1 - 21B.6 Bildgröße, optimaler Standpunkt 13:35
- 22B.1 Tangentengerade an sin(x²) 15:56
- 22B.2 ln(3) mit linearer Näherung schätzen 8:29
- 22B.3 Tangentengeraden durch Ursprung an Parabel 9:17
- 22B.4 lineare Näherung für kleine Drehung 18:41
- 22B.5 Linsengleichung auflösen; Fehlerrechnung; lineare Näherung 10:43
- 23B.1 Integrale mit Sinus und Partialbruchzerlegung 17:41
- 23B.2 Stammfunktion der Betragsfunktion 3:48
- 24B.1 partielle Integration; Fingerübung 7:34
- 24B.2 partielle Integration; Logarithmus integrieren 2:27
- 24B.3 doppelte partielle Integration; x Quadrat mal Sinus 5:38
- 24B.4 Integration durch Substitution; Fingerübung 8:04
- 24B.5 Integration durch Substitution; weitere Fingerübung 9:04
!1 - 24B.6 drei Wege für Integration durch Substitution 11:27
- 25B.1 Bogenlänge einer Funktionskurve, Beispiel 8:42
- 25B.2 Rotationskörper; Volumen bei Drehung um x- und um y-Achse 19:46
!1 - 25B.3 Rotationskörper; Mantelfläche bei Drehung um x-Achse 8:58
- 25B.4 Rotationskörper; Mantelfläche bei Drehung um y-Achse 6:53
- 25B.5 Schwerpunkt einer halben Kreisscheibe 11:47
- 26B.1 Wahrscheinlichkeit; dreimal würfeln, mindestens eine Sechs 13:07
- 26B.2 Wahrscheinlichkeit; einmal Kopf mit idealer Münze und gezinkter Münze 3:39
- 26B.3 Wahrscheinlichkeit; Buchstaben für Wort ziehen 2:52
!1 - 26B.4 Wahrscheinlichkeit; hundert Bauteile, mindestens eines defekt 15:32
- 26B.5 Wahrscheinlichkeit; niemand im Laden 7:45
- 26B.6 Wahrscheinlichkeit; Bayes; Verspätung und schlechtes Wetter 6:18
- 26B.7 idealer und defekter Würfel; unabhängige und unvereinbare Ereignisse 7:41
- 26B.8 überraschende Wahrscheinlichkeiten; Mädchen am Montag 14:00
!1 - 27B.1 Erwartungswert; Würfel, der vom Tisch fällt 7:40
- 27B.2 Erwartungswert; Summe Würfel und Münze 6:45
!1 - 27B.3 Erwartungswert; Flieger überbuchen oder nicht 25:54
!1 - 27B.4 Erwartungswert einer stetigen Zufallsgröße 10:37
- 27B.5 Varianz, Standardabweichung; drei Münzen 13:53
!1 - 27B.6 Varianz, Standardabweichung; stetige Zufallsgröße 16:19
- 27B.7 Normierung Wahrscheinlichkeitsdichte; Median einer stetigen Zufallsgröße 6:26
- 27B.8 Wahrscheinlichkeitsdichte; Erwartungswert, Varianz, Standardabweichung 12:02
- 27B.9 gleichmäßige Verteilung; Standardabweichung 7:20
- 27B.10 Lebensdauer eines radioaktiven Atoms, Wahrscheinlichkeitsdichte 16:21
- 27B.11 Beispiel Quartile einer Wahrscheinlichkeitsdichte 8:10
- 27B.12 Münze prüfen, ob ideal; Nullhypothese 6:28
- 27B.13 Zahl zerfallender Atome pro Sekunde 11:14
- 27B.14 gegebene Zahl an Atomen pro Sekunde soll zerfallen 6:07
- 27B.15 Erwartungswert eines Produkts unkorrelierter Zufallsgrößen 5:40
- 28B.1 drei Münzen; Erwartungswert der Standardabweichung der Stichprobe 18:46
- KB.00 Operationen, die Summen bzw. Produkte respektieren 12:25
- KB.01 Beispiel Partialbruchzerlegung 15:58
- KB.02 Beispiel Grenzwert 9:36
- KB.03 Beispiel Funktionskurve skizzieren 6:11
- KB.04 Beispiel Ableitung 1:13
- KB.05 Was ist 2 hoch i 2:21
- KB.06 Beispiel Wurzeln und Potenzen auflösen 2:20
- KB.07 Beispiel rechtwinkliges Dreieck 2:31
- KB.08 Beispiel Nullstellen im Komplexen 2:36
- KB.09 Beispiel Exponentialfunktion bestimmen 4:19
- KB.10 Beispiel partielle Integration 4:41
- KB.11 (a-b+c) hoch 42 auflösen 2:50
- KB.12 Beispiel Linearfaktorzerlegung, komplexe Zahlen 2:02
- KB.13 Beispiel Integration durch Substitution 4:07
- KB.14 Zahl der Spiele bei Turnier jeder gegen jeden 5:06
- KB.15 Maximum kubische Parabel 3:52
- KB.16 Produkt mit komplexer Zahl gegeben 1:34
- KB.17 komplexe Zahl hoch 6 ist i 4:50
- KB.18 Integral einer rationalen Funktion 1:31
- KB.19 Asymptotengerade einer rationalen Funktion 2:01
- KB.20 Integral einer rationalen Funktion, anderes Beispiel 8:52
- KB.21 Beispiel Ableitungsregeln 1:40
- KB.22 Sinus vom siebenfachen Winkel mit Eulerscher Identität 4:59
- KB.23 Gleichung mit Logarithmus und Potenz 2:03
- KB.24 dritte Potenz einer komplexen Zahl ist 8 3:14
- KB.25 kleinster Wert einer Parabel 1:27
- KB.26 Beispiel Substitutionsregel; Wurzel 1:49
- KB.27 quadratische Ungleichung 2:57
- KB.28 Standardabweichung der Lebensdauer 14:14
- KB.29 Ungleichung mit einfacher rationaler Funktion 4:22
- KB.30 einfache Partialbruchzerlegung 3:14
Mathe 1, Winter 2013/2014
21:36:55
- 01C.1 Zerlegung einer Kraft in zwei Richtungen 36:37
- 02C.1 Ableitungen ausrechnen, Beispiele; Kettenregel; Produktregel 23:34
- 02C.2 Schätzung der Fehlergrenze für das Würfelvolumen per Ableitung 13:47
- 02C.3 Unterschied Terabyte dezimal zu binär mit Ableitung schätzen 13:13
- 02C.4 radioaktiven Zerfall mit Ableitung schätzen 19:10
!1 - 03C.1 Beispiele für Folge und logische Äquivalenz; hinreichend, notwendig 18:09
- 03C.2 Fehler bei Äquivalenzumformungen 5:00
- 03C.3 Beispielaufgaben zu Mengen 10:07
- 03C.4 Tortenstück im R² als Menge schreiben 9:58
- 03C.5 Beispiel für Menge im R² mit Parabel 1:05
- 04C.1 Binärzahlen; ein Zehntel binär schreiben 21:20
- 04C.2 Beispiel für dritte Potenz einer komplexen Zahl 12:09
- 04C.3 quadratische Gleichung mit komplexen Zahlen lösen 3:52
- 05C.1 Ungleichung mit Quadrat im Nenner lösen 33:15
!1 - 06C.1 Wahrscheinlichkeit, Würfel sechsmal werfen, alle Zahlen 8:17
- 06C.2 mittels Binomialkoeffizienten (a-b) hoch 5 ausmultiplizieren 9:08
- 06C.3 Wahrscheinlichkeit für ABC in fünf gezogenen Buchstaben 6:09
- 06C.4 Wiederholung Kombinatorik; Ausmultiplizieren; Zahl an PIN-Nummern 14:37
!1 - 06C.5 Wiederholung Kombinatorik; Farbmuster; jeder gegen jeden; Zubehörteile 11:15
- 07C.1 Bildmengen von vier Beispielfunktionen 12:53
- 07C.2 Zahl der möglichen Abbildungen von einer nach einer anderen gegebenen Menge 9:51
- 07C.3 kompliziertere Bildmenge im R² 27:34
- 07C.4 rekursiv definierte Funktion explizit machen 13:30
- 07C.5 Beispiel für Bildmenge eines Polynoms 6:46
- 08C.1 Ideen hinter dem mathematischen Begriff Relation 14:50
- 08C.2 Bezeichnung f hoch -1 für die Umkehrfunktion 7:05
- 08C.3 Beispiele für kartesische Produkte 9:12
- 08C.4 Funktionen umkehrbar oder nicht 16:49
!1 - 09C.1 Beispiele für monotone, gerade, ungerade, periodische Funktionen 27:13
- 09C.2 Potenzen, Wurzeln vereinfachen 6:50
- 09C.3 Geradengleichung mit Einheiten 8:28
- 09C.4 Summe aus Quadrat oder Wurzel holen 8:30
- 09C.5 eine gerade Funktion mit Periode 4 bauen 5:16
- 09C.6 streng monotone Funktion durch drei Punkte bauen 6:21
!1!2!3 - 09C.7 Sind diese Funktionen monoton, (un)gerade, periodisch, umkehrbar 8:55
- 10C.1 einige Potenzen und Logarithmen schätzen 26:31
- 10C.2 einige Potenzen und Wurzeln vereinfachen 2:02
- 10C.3 einige Logarithmen und Potenzen umformen 9:12
- 10C.4 Zehner- und natürlicher Logarithmus gemischt 6:15
- 10C.5 Exponentialfunktion wächst über Potenzfunktion 11:50
- 10C.6 Zinseszins mit Eulerscher Zahl schätzen 3:08
- 10C.7 Beispiele zum Auflösen von Potenzen und Logarithmen 4:00
- 10C.8 Zinssatz zu Zinseszins bestimmen 4:09
- 12C.1 Zahl der Lösungen einer quadratischen Gleichung 10:18
- 12C.2 kubische Gleichung allgemein lösen 24:56
- 13C.1 rationale Funktionen skizzieren; Nullstellen; Polstellen; schräge Asymptote 34:40
!1 - 13C.2 rationale Funktion mit vorgegebener Nullstelle, Polstelle, Asymptote 12:28
!1 - 13C.3 rationale Funktion mit vorgegebener Nullstelle, Polstelle, vorgegebenem y-Achsenabschnitt 8:47
- 13C.4 rationale Funktion mit vorgegebener Nullstelle und schräger Asymptote, ohne Polstelle 3:14
!1 - 13C.5 Skizze einer rationalen Funktion 6:20
!1!2 - 14C.1 Beispiele für Partialbruchzerlegung 19:40
- 14C.2 weiteres Beispiel für Partialbruchzerlegung 5:01
- 15C.1 Funktionskurven stauchen, verschieben, spiegeln usw. an Beispielen 19:07
- 16C.1 Winkel eines Dreiecks, wenn alle Seitenlängen gegeben 5:40
- 17C.1 Winkel und Betrag einiger komplexer Zahlen; Arkustangens 13:52
- 17C.2 komplexe Zahlen multiplizieren und dividieren, algebraisch und geometrisch 15:14
!1!2 - 17C.3 Komplexe Zahlen multiplizieren heißt Längen multiplizieren und Winkel addieren 6:22
- 17C.4 Rechnen mit komplexen Zahlen, die als Länge und Winkel gegeben sind 19:23
!1 - 17C.5 Bildmenge eines komplexwertigen Bruchs 5:22
- 18C.1 Beispiel für komplexwertige Nullstellen eines Polynoms 4:29
- 19C.1 Beispiele für beschränkte, monotone, konvergente Folgen 17:59
- 19C.2 Grenzwerte von komplizierteren Folgen 12:58
!1 - 19C.3 Grenzwerte von komplizierteren Funktionen 24:41
- 19C.4 Grenzwerte von rekursiv definierten Folgen 9:56
- 19C.5 Unendliche Rekursion von sin x plus usw. soll 1 ergeben 2:18
- 20C.1 Ableitung von Sinus und Cosinus mittels e und komplexen Zahlen 11:22
- 20C.2 einige Ableitungen nach Rezept 15:03
- 20C.3 Netz-Wechselspannung ableiten 9:50
- 20C.4 idealer Kondensator an Netzspannung 15:21
!1 - 20C.5 Ableitungsregeln angewendet 1:58
- 21C.1 Beispiele für lokale Maxima, Minima; Wendepunkte 17:32
!1 - 21C.2 Funktion bauen, die an gegebenen Stellen lokale Minima hat 15:20
!1 - 21C.3 lokale Maxima, lokale Minima, Wendepunkte von Sinus, Cosinus, Tangens 20:48
!1 - 22C.1 Tangentengerade an Einheitskreis 20:11
- 23C.1 einfache Integrale per Stammfunktion 9:08
- 23C.2 Beispiel für Trapezregel und Simpsonregel 19:05
- 23C.3 Fläche zwischen Sinus- und Cosinus-Kurve 6:37
- 23C.4 einfache Differentialgleichungen; Wurfparabel 10:35
- 23C.5 Parabel mit gegebener Füllhöhe 7:12
- 23C.6 Integral über Polstelle hinweg 9:14
!1 - 24C.1 Anwendungen der Integrationsregeln 36:30
!1 - 24C.2 weitere Anwendungen der Integrationsregeln 13:10
!1 - 24C.3 Stammfunktionen für Betrag und für Sinus vom Betrag 7:45
- 25C.1 Flächeninhalt und Umfang einer Ellipse; Bogenlänge 22:00
- 25C.1 Rotationskörper aus Hyperbel; Volumen, Mantelfläche 23:33
!1!2 - 26C.1 ideale oder nichtideale Münze fünfmal werfen 36:19
- 27C.1 Zufallsgröße aus Würfel und Münze 11:00
- 27C.2 hunderttausend Bauteile, sieben kaputt 18:40
- 27C.3 Geigerzähler; Poisson-Verteilung 12:16
- 27C.4 Erwartungswert und erstes Quartil aus Wahrscheinlichkeitsdichte 12:48
- 28C.1 Erwartungswert, Varianz, Standardabweichung für eine diskrete und eine stetige Verteilung 18:35
!1 - 28C.2 Erwartungswert, Varianz, Standardabweichung von drei Münzen 13:13
- 29C.1 Varianz und Standardabweichung aus Stichprobe 15:36
!1 - 29C.2 Wahrscheinlichkeitsdichte an Stichprobe anpassen, Teil 1 18:05
- 29C.3 Wahrscheinlichkeitsdichte an Stichprobe anpassen, Teil 2 37:32
Mathe 1, Winter 2015/2016
13:04:14
- Vektoren und Vektorräume, Teil 1; Vektoraddition 34:04
- Vektoren und Vektorräume, Teil 2; Multiplikation mit Zahlen 31:09
- Vektoren als Pfeile und in Zahlen addieren 6:59
- Einige kleine Beweise in der Linearen Algebra 18:28
!1!2 - Vektoren zerlegen, Basis, Dimension 29:33
!1 - Einen Vektor in drei gegebene Vektoren zerlegen 8:27
- Noch einen Vektor in drei gegebene Vektoren zerlegen, Sonderfall 5:46
- Länge von Vektoren, Pythagoras 14:42
- Skalarprodukt, mechanische Arbeit 25:38
- Vektorprodukt, Kreuzprodukt 27:44
- Drei verschiedene Produkte mit Vektoren 6:41
- Zusammenhang zwischen Skalarprodukt und Länge 1:36
- Satz des Pythagoras mit Vektoren schreiben 5:18
!1 - Skalarprodukt testet, ob Vektoren zueinander senkrecht 10:21
!1 - Skalarprodukt per Zerlegung in parallelen und senkrechten Anteil 11:17
- Skalarprodukte einiger Vektoren geometrisch 10:21
!1 - Proportionalität, proportionale Funktionen 24:03
- Lineare Funktionen 6:03
- Potenzen, Potenzfunktionen 25:52
!1!2 - Polynome 9:02
- Wurzeln, gebrochenzahlige Potenzen 42:01
- Wurzelausdrücke vereinfachen 7:52
!1 - Exponentialfunktionen 6:43
- Logarithmen 22:25
- Logarithmus zu anderer Basis 5:38
- Annuitätenrechnung, Ratenzahlung 30:37
- Einige Logarithmen schätzen 10:52
- Winkel im Bogenmaß 4:57
- Sinus, Cosinus, Tangens 7:28
!1 - sin, cos, tan für 0°, 30°, 45°, 60°, 90° 10:25
- Sinus, Cosinus am Einheitskreis 16:27
!1!2 - Arkussinus, Arkuscosinus, Arkustangens 20:37
- Inkreis eines rechtwinkligen Dreiecks mit den Seitenlängen 3, 4, 5 11:09
- Summe der Innenwinkel eines Vielecks 8:02
!1 - Fläche von Kreis in Viereck in Kreis und umgekehrt; Skalierung von Fläche und Volumen 12:22
- Fläche eines Dreiecks; Sinussatz 9:36
- Cosinussatz 9:45
- Beispiele für Sinussatz, Cosinussatz 15:42
- a sin(bx + c) + d 14:00
- Ableitung als Tangentensteigung und als Änderungsrate 25:30
!1!2 - Ableitung als Bestandteil der linearen Näherung 26:48
- Ableitung der Wurzelfunktion, noch ohne Ableitungsregeln 5:24
- Summen und Produkte ableiten 11:43
- Kettenregel 22:16
!1!2 - e-Funktion, Ableitung von e-Funktion und natürlichem Logarithmus 15:09
- Ableitung von Potenzfunktionen und vom Kehrwert 6:18
- Quotientenregel 4:33
- Ableitung des Sinus 7:21
- x^3 und 3^x und x^x ableiten 15:59
- Wurzel(4,01) mittels linearer Näherung 10:16
- Radioaktiver Zerfall, Modell mit Ableitung 16:10
- Senkrechter Wurf und freier Fall, Modell mit Ableitung 12:52
- Integral; Hauptsatz der Differential- und Integralrechnung 24:13
Mathe 1, Winter 2016/2017
10:54:15
- 03D.1 Mengenoperationen mit Zahlen und Geometrie 24:05
- 03D.2 logische Folge mit Wahrheitstabelle nachweisen 6:15
- 04D.1 Addition und Multiplikation im Dualsystem; Dualbrüche 13:37
- 04D.2 schriftlich dividieren; periodischen Dezimalbruch als gewöhnlichen Bruch schreiben 11:35
- 04D.3 Mengenoperationen mit Zahlenintervallen 4:24
- 05D.1 Ungleichungen mit Quadrat und mit Betrag lösen 33:39
- 06D.1 Beispiele für Fakultät, Binomialkoeffizent usw. 27:58
- 06D.2 Binomialkoeffizenten am Beispiel (a+b)^7 2:50
- 07D.1 Begriffe zu Funktionen; Funktionen mehrerer Veränderlicher 29:46
- 08D.1 Beispiele für Umkehrfunktionen 32:20
- 09D.1 einige Gleichungen mit Potenzen auflösen 10:19
- 09D.2 gerade, ungerade, monoton, periodisch; Beispiele für Funktionen angeben 10:45
- 09D.3 Zwischenwert linear schätzen 3:36
- 09D.4 Ausdrücke mit Potenzen und Wurzeln umformen 15:58
- 09D.5 Zweierpotenzen schätzen; Billion deutsch und englisch 5:18
- 10D.1 doppeltlogarithmisches Diagramm für Potenz- und Polynomfunktion 7:04
- 11D.1 aus der Linearfaktorzerlegung den Graphen einer Polynomfunktion ablesen 15:10
- 11D.2 Beispiele für Linearfaktorzerlegung 9:26
- 13D.1 einige rationale Funktionen skizzieren 29:57
- 14D.1 rationale Funktion aus Nullstelle, Polstelle, Asymptote 14:47
- 14D.2 Beispiel für Partialbruchzerlegung 13:56
!1 - 15D.1 Skizziere 3sin(2x+1)+4, Sinus in Betrag, Sinus in Potenz 23:07
- 17D.1 Grundrechenarten für komplexe Zahlen am Beispiel; Länge, Winkel 21:31
- 18D.1 die fünften Wurzeln einer komplexen Zahl 14:55
- 18D.2 quadratische Gleichung mit komplexen Zahlen 6:06
- 18D.3 Kehrwert, Potenz, Wurzel, Logarithmus einer komplexen Zahl in Polarform 24:16
- 19D.1 Beispiele für Grenzwerte von Brüchen 9:25
- 20D.1 einige Ableitungsaufgaben von Wurzeln bis zum Arcuskosinus 23:51
- 21D.1 Beispiel für Kriterieren für lokale Maxima und Minima, Wendestellen 22:25
!1 - 21D.2 weiteres Beispiel für Kriterieren für lokale Maxima und Minima, Wendestellen 9:49
- 21D.3 Reichweite des schiefen Wurfs maximieren 27:15
- 23D.1 unbestimmtes und bestimmtes Integral einer stückweise definierten Funktion 14:18
- 24D.1 Gamma-Funktion; partielle Integration 13:58
- 24D.2 partielle Integration und Substitutionsregel am Beispiel 15:35
- 27D.1 Binomialverteilung; Bedeutung und Berechnung des Erwartungswerts 34:25
- 27D.2 Warteschlange, Wahrscheinlichkeiten und Erwartungswert 38:01
- 29D.1 Varianz der Grundgesamtheit und der Stichprobe 32:33
Mathe 2 Teil 1, Sommer 2010
27:41:40
- 01.01.1 Überblick: Lineare Algebra 10:41
- 01.01.2 Überblick: Lineare Algebra 8:11
- 01.02.1 Überblick: Dynamische Systeme, Differentialgleichungen 9:11
- 01.02.2 Überblick: Dynamische Systeme, Differentialgleichungen 8:27
- 01.03.1 Überblick: Potenzreihen 8:26
- 01.03.2 Überblick: Potenzreihen 8:35
- 01.04.1 Überblick: Fourier-Reihe 5:58
- 01.04.2 Überblick: Fourier-Transformation 6:10
- 01.04.3 Überblick: Laplace-Transformation 8:07
- 01.05.1 Überblick: Funktionen mehrerer Veränderlicher 8:42
- 01.05.2 Überblick: Funktionen mehrerer Veränderlicher 7:49
- 02.01.1 Rechnen mit Pfeilen 10:37
!1!2 - 02.01.2 Rechnen mit Pfeilen 3:14
!1 - 02.02 Schreibweise Vektoren 2:38
- 02.03.1 Gerichtete und ungerichtete Größen 8:02
- 02.03.2 Gerichtete und ungerichtete Größen 8:43
- 02.04.1 Ebene R2 und Raum R3 8:07
- 02.04.2 Ebene R2 und Raum R3 3:57
- 02.04.3 Ebene R2 und Raum R3 3:54
- 02.04.4 Ebene R2 und Raum R3 4:26
- 02.05.1 Begriff Vektorraum 7:40
- 02.05.2 Begriff Vektorraum 5:47
- 02.06 Basis, Dimension 10:43
- 03.01 Begriff Matrix 8:22
- 03.02 Matrixoperationen 10:49
- 03.03.1 Matrixprodukte 9:19
- 03.03.2 Matrixprodukte 8:58
- 03.03a Matrizen in MATLAB(R) 6:35
- 03.03b Matrizen in Wolfram Alpha 2:29
- 03.04 Skalierung 5:16
- 03.05 Drehung 10:45
- 03.05a Drehung in MATLAB(R) 7:31
!1 - 03.06 Verschiebung 5:35
- 04.01 Vorbemerkung Länge und Skalarprodukt 3:09
- 04.02 Euklidische Länge 9:37
!1 - 04.03.1 Skalarprodukt 6:55
- 04.03.2 Skalarprodukt, Länge, Orthogonalität 10:29
- 04.03.3 Skalarprodukt 9:47
- 04.03.4 Skalarprodukt, Cosinussatz 10:14
- 04.04.1 Parametrische Geradengleichungen, Punkt-Richtungs-Form 10:18
- 04.04.2 Parametrische Geradengleichungen, Punkt-Richtungs-Form, Zwei-Punkt-Form 10:33
- 04.05 Geradengleichung in Normalenform 9:56
- 05.01.1 Lineare Gleichungssysteme 8:24
- 05.01.2 Lineare Gleichungssysteme 10:09
!1 - 05.02.1 Existenz von Lösungen linearer Gleichungssysteme 7:04
- 05.02.2 Existenz von Lösungen linearer Gleichungssysteme 5:24
- 05.03.1 Bild und Rang einer Matrix 9:30
- 05.03.2 Bild und Rang einer Matrix 7:54
- 05.04 Eindeutigkeit von Lösungen linearer Gleichungssysteme 5:41
- 05.05 Kern und Defekt einer Matrix 10:07
- 05.06.1 Existenz und Eindeutigkeit von Lösungen linearer Gleichungssysteme 10:12
- 05.06.2 Existenz und Eindeutigkeit von Lösungen linearer Gleichungssysteme 8:40
- 05.A.1 Wiederholung Bild und Rang 8:31
- 05.A.2 Wiederholung Bild und Rang 7:05
- 05.B.1 Wiederholung Kern und Defekt 6:01
- 05.B.2 Wiederholung Kern und Defekt 6:14
- 06.01.1 Determinante, Idee 10:21
!1 - 06.01.2 Determinante, Ergebnisse ohne Rechnen 10:18
!1 - 06.01.3 Determinante, Ergebnisse ohne Rechnen 6:48
- 06.01.4 Determinante, Rechenregeln 10:21
!1!2 - 06.01.5 Determinante, 2×2 ausrechnen 8:59
- 06.01.6 Determinante, Entwicklung, Sarrus 9:49
!1!2!3 - 06.01a Kennzahlen für Matrizen 8:16
- 06.02 Spatprodukt 9:51
- 06.03.1 Vektorprodukt 10:36
- 06.03.2 Vektorprodukt 10:45
- 06.03.3 Vektorprodukt 3:45
- 06.04.1 Geometrie des Vektorprodukts 9:46
- 06.04.2 Geometrie des Vektorprodukts 7:17
- 06.04.3 Geometrie des Vektorprodukts 10:24
- 06.04.4 Geometrie des Vektorprodukts 7:15
- 06.05 Zusammenfassung: Produkte mit Vektoren 8:23
!1!2!3!4 - 06.06.1 Inverse Matrix 10:16
- 06.06.2 Inverse Matrix 10:55
- 07.01.1 Cramer-Verfahren 10:42
- 07.01.2 Cramer-Verfahren 5:09
- 07.02.1 Gaußsches Eliminationsverfahren 7:03
- 07.02.2 Gaußsches Eliminationsverfahren 10:43
- 07.03 Jacobi-Verfahren 10:39
- 07.04. Lineare Gleichungssysteme mit Standardsoftware 8:42
!1 - 08.01.1 Eigenwerte und Eigenvektoren, Begriff 8:38
!1 - 08.01.2 Eigenwerte und Eigenvektoren, Begriff 10:47
- 08.01.3 Eigenwerte und Eigenvektoren, Begriff 10:16
- 08.02.1 Eigenwerte und Eigenvektoren, Anwendungen 10:35
- 08.02.2 Eigenwerte und Eigenvektoren, Anwendungen 3:47
!1 - 08.03.1 Bestimmung von Eigenwerten 10:41
- 08.03.2 Bestimmung von Eigenwerten 7:49
- 08.03.3 Bestimmung von Eigenwerten 7:17
- 09.01.1 Dynamische Systeme, Begriff 10:41
- 09.01.2 Dynamische Systeme, Begriff 10:32
- 09.02.1 Logistische Gleichung, ein einfaches dynamisches System 10:12
!1!2 - 09.02.2 Logistische Gleichung, ein einfaches dynamisches System 10:46
- 09.02.3 Logistische Gleichung, ein einfaches dynamisches System 1:40
- 09.03.1 Typen von Differentialgleichungen 10:32
- 09.03.2 Typen von Differentialgleichungen 7:27
- 09.04.1 Federpendel, Vektorfelder und Lösungskurve 9:03
!1 - 09.04.2 Federpendel, Vektorfelder und Lösungskurve 6:28
- 09.04.3 Federpendel, Vektorfelder und Lösungskurve 10:41
- 09.04.4 Federpendel, Vektorfelder und Lösungskurve 3:21
- 10.01 Lösung von Differentialgleichungen durch Ansatz 7:26
- 10.02 Homogene lineare Differentialgleichung erster Ordnung mit konstanten Koeffizienten 9:51
- 10.03.1 Inhomogene lineare Differentialgleichung erster Ordnung mit konstanten Koeffizienten 10:24
- 10.03.2 Inhomogene lineare Differentialgleichung erster Ordnung mit konstanten Koeffizienten 10:39
- 10.03.3 Inhomogene lineare Differentialgleichung erster Ordnung mit konstanten Koeffizienten 10:40
!1!2 - 10.04.1 Variation der Konstanten 10:40
- 10.04.2 Variation der Konstanten 4:05
- 10.05.1 Homogene lineare Differentialgleichung zweiter Ordnung mit konstanten Koeffizienten 10:39
- 10.05.2 Homogene lineare Differentialgleichung zweiter Ordnung mit konstanten Koeffizienten 10:56
- 10.05.3 Homogene lineare Differentialgleichung zweiter Ordnung mit konstanten Koeffizienten 10:40
- 10.05.4 Homogene lineare Differentialgleichung zweiter Ordnung mit konstanten Koeffizienten 3:23
- 10.06 Inhomogene lineare Differentialgleichung zweiter Ordnung mit konstanten Koeffizienten 10:08
- 11.00.1 Zusammenfassung Differentialgleichungen 9:09
- 11.00.2 Zusammenfassung Differentialgleichungen 9:22
- 11.01.1 Differentialgleichungen mit trennbaren Variablen 10:49
- 11.01.2 Differentialgleichungen mit trennbaren Variablen 10:54
- 12.01.1 Numerische vs. analytische Lösung von Differentialgleichungen 8:34
!1 - 12.01.2 Numerische Lösung von Differentialgleichungen 3:17
- 12.01.3 Numerische vs. analytische Lösung von Differentialgleichungen 5:59
- 12.01.4 Numerische vs. analytische Lösung von Differentialgleichungen 6:17
!1 - 12.01a.1 nochmal Klassifikation von Differentialgleichungen 9:12
- 12.01a.2 nochmal Klassifikation von Differentialgleichungen 8:26
- 12.02.1 Explizites Euler-Verfahren 10:35
- 12.02.2 Explizites Euler-Verfahren 6:03
!1 - 12.02.3 Implizites Euler-Verfahren 8:18
!1!2!3!4 - 12.02.4 Implizites Euler-Verfahren 3:15
!1!2 - 12.03.1 Symplektisches Euler-Verfahren 9:21
- 12.03.2 Symplektisches Euler-Verfahren 10:22
- 13.01.1 höhere Ordnung in DGL-System umwandeln 9:09
- 13.01.2 höhere Ordnung in DGL-System umwandeln 5:29
- 13.02.1 Differentialgleichungen mit MATLAB(R) lösen 9:07
!1 - 13.02.2 Differentialgleichungen mit MATLAB(R) lösen 5:46
- 13.02.3 Differentialgleichungen mit MATLAB(R) lösen 8:05
- 14.01.1 DGL-Systeme mit Eigenvektoren lösen 10:54
- 14.01.2 DGL-Systeme mit Eigenvektoren lösen 8:55
- 14.01.3 DGL-Systeme mit Eigenvektoren lösen 10:44
- 14.01.4 DGL-Systeme mit Eigenvektoren lösen 7:40
- 14.01a Wiederholung homogene lineare Differentialgleichungen mit konstanten Koeffizienten 9:04
- 14.02.1 Exponentialfunktion von Matrizen 7:37
- 14.02.2 Exponentialfunktion von Matrizen 10:41
- 14.02.3 Exponentialfunktion von Matrizen mit MATLAB(R) 4:56
- 15.01.1 Tangentengerade, Schmiegeparabel 7:37
- 15.01.2 Tangentengerade, Schmiegeparabel 10:53
!1 - 15.02.1 Taylor-Polynome, Anwendung 10:04
- 15.02.2 Taylor-Polynome, Anwendung 9:58
- 15.02.3 Taylor-Polynome in Wolfram Alpha 8:05
- 15.03.1 Taylor-Reihe 10:53
- 15.03.2 Taylor-Reihe, Eulersche Identität 5:49
- 15.03.3 Taylor-Reihe, Problemfall 9:57
- 15.03.4 Taylor-Reihe, Problemfall 9:00
- 15.03.5 Taylor-Reihe, Problemfall 5:30
- 16.01 Taylor-Polynome Rest 9:46
!1 - 16.02.1Taylor-Restformel 9:48
- 16.02.2 Taylor-Restformel 10:27
!1 - 16.03.1 Taylor-Rest Abschätzung 8:58
- 16.03.2 Taylor-Rest Abschätzung 10:22
- 16.04.1 Taylor-Rest, Beispiel 10:31
- 16.04.2 Taylor-Rest, Beispiel 7:12
- 17.01.1 Taylor-Reihe, Potenzreihe 10:26
- 17.01.2 Taylor-Reihe, Potenzreihe 5:15
- 17.02.1 Konvergenz von Potenzreihen 10:21
- 17.02.2 Konvergenz von Potenzreihen 9:08
- 17.03 Konvergenzradius 10:34
- 17.04 Analytische Funktion 10:10
- 17.05.1 Lösen von Differentialgleichungen mit Potenzreihen 9:11
- 17.05.2 Lösen von Differentialgleichungen mit Potenzreihen 7:01
- 18.01.1 Fourier, Überlagerung sinusförmiger Wellen 9:48
!1!2 - 18.01.2 Fourier, Überlagerung sinusförmiger Wellen 4:47
- 18.01.3 Fourier, Überlagerung sinusförmiger Wellen 4:49
- 18.02.1 Fourier, Funktionen mit der Periode 1 8:52
- 18.02.2 Fourier, Funktionen mit der Periode 1 10:11
- 18.02.3 Fourier, Funktionen mit der Periode 1 9:15
- 18.02.4 Fourier, Funktionen mit der Periode 1 6:02
- 18.03.1 Fourier-Reihe mit komplexer Exponentialfunktion 9:55
- 18.03.2 Fourier-Reihe mit komplexer Exponentialfunktion 10:17
- 18.03.3 Fourier-Reihe mit komplexer Exponentialfunktion 10:19
- 18.03.4 Fourier-Reihe mit komplexer Exponentialfunktion 5:35
- 18.04 Fourier-Reihe, Vollständigkeit 6:55
- 18.05 Fourier-Reihe, Funktionen mit Periode T 9:56
- 19.01.1 Fourier-Reihe mit Sinus und Cosinus 9:59
- 19.01.2 Fourier-Reihe mit Sinus und Cosinus 5:43
- 19.02.1 Fourier-Koeffizienten für Sinus und Cosinus 7:50
- 19.02.2 Fourier-Koeffizienten für Sinus und Cosinus 10:10
!1!2!3 - 19.02.3 Fourier-Koeffizienten für Sinus und Cosinus 6:28
- 19.03.1 Diskrete Fourier-Transformation, FFT 10:53
- 19.03.2 Diskrete Fourier-Transformation, FFT 8:25
- 20.01.1 Kontinuierliche Fourier-Transformation 9:14
- 20.01.2 Kontinuierliche Fourier-Transformation 7:58
!1!2!3!4!5!6!7 - 20.01.3 Kontinuierliche Fourier-Transformation 8:12
- 20.02.1 Kontinuierliche Fourier-Analyse und -Synthese 8:26
- 20.02.2 Kontinuierliche Fourier-Analyse und -Synthese 10:33
- 20.02.3 Kontinuierliche Fourier-Analyse und -Synthese 2:43
- 20.03 Laplace-Transformation 10:49
- 20.04 Laplace-Transformation von Ableitungen 9:56
- 20.05.1 Laplace-Transformation von exp, sin, cos 7:09
- 20.05.2 Laplace-Transformation von exp, sin, cos 9:08
- 20.06 Laplace-Transformation von Potenzfunktionen 9:54
!1 - 20.07 Laplace-Transformation von verzögerten oder zeitskalierten Funktionen 9:06
- 20.08 Funktionaltransformationen, Fourier, Laplace, z 3:51
- weiter in Playlist Mathe 2 RE Teil 2, Sommer 2010 0:11
Mathe 2 Teil 2, Sommer 2010
6:10:56
- 21.01.1 Differentialgleichungen per Lapace-Transformation 9:20
- 21.01.2 Ableitungen in Produkte verwandeln 9:29
- 21.02.1 von der Laplace-Transformation zur Lösung 10:51
- 21.02.2 von der Laplace-Transformation zur Lösung 9:34
- 22.01.1 Funktionen mehrerer Veränderlicher, MATLAB(R) 10:34
- 22.01.2 Funktionen mehrerer Veränderlicher, MATLAB(R) 8:41
!1!2 - 22.01.3 Funktionen mehrerer Veränderlicher, MATLAB(R) 10:58
- 22.02 Definitionsbereich und Bild bei mehreren Veränderlichen 7:05
- 23.01.1 partielle Ableitungen 8:07
- 23.01.2 Gradient 7:32
- 23.01.3 Gradient in MATLAB(R) 10:13
- 23.01.4 Gradient in MATLAB(R) 2:41
- 23.01.5 Gradient und partielle Ableitung 10:05
!1!2!3 - 23.01.6 mehrfache partielle Ableitungen 3:08
!1!2!3 - 23.02.1 Tangentialebene, lineare Näherung 10:34
- 23.02.2 Tangentialebene, lineare Näherung 10:58
- 24.01.1 Fehlerfortpflanzung, Größtfehler 9:57
- 24.01.2 Fehlerfortpflanzung, Größtfehler 10:57
- 24.02.1 Fehlerfortpflanzung, Standardabweichung 10:05
- 24.02.2 Fehlerfortpflanzung, Standardabweichung 10:59
- 24.03.1 Minima, Maxima, mehrere Veränderliche 10:20
- 24.03.2 Minima, Maxima, mehrere Veränderliche 7:33
- 24.03.3 Maxima, mehrere Veränderliche 10:29
- 24.03.4 Maxima, mehrere Veränderliche 10:03
- 24.03.5 Maxima, mehrere Veränderliche 2:58
!1 - 24.03.6 Maxima, mehrere Veränderliche 5:16
- 25.01 Polar-, Zylinder-, Kugelkoordinaten, Zweck 1:48
- 25.02 Polarkoordinaten 6:56
- 25.03 Zylinderkoordinaten 4:17
- 25.04.1 Kugelkoordinaten, sphärische Koordinaten 8:08
!1 - 25.04.2 Kugelkoordinaten, sphärische Koordinaten 9:49
!1!2 - 26.01 Mehrfachintegral, Idee 10:48
- 26.02.1 Mehrfachintegral kartesisch 6:35
- 26.02.2 Mehrfachintegral kartesisch 10:56
- 26.03.1 Integral in Polarkoordinaten 7:47
- 26.03.2 Kreisfläche in Polarkoordinaten 6:26
- 26.04.01 Integral Kugelkoordinaten 10:13
- 26.04.02 Kugelvolumen sphärische Koordinaten 7:11
- 26.05 Kurvenintegral 6:27
!1 - A01.01 Diffusionsgleichung Wärmeleitung 10:19
- A01.02 Diffusionsgleichung Wärmeleitung MATLAB(R) 7:05
- A01.03 Diffusionsgleichung Wärmeleitung 4:57
- A01.04 Wellengleichung, Waveguide Synthesis 9:35
- A01.05 Wellengleichung, Waveguide Synthesis, Karplus-Strong, MATLAB(R) 9:44
!1!2 - A01.06 Wellengleichung, Waveguide Synthesis, Sonification 3:28
!1!2!3!4
Mathe 2, Sommer 2011
27:02:57
- 01.1 Überblick 2. Semester; Lineare Algebra, Differentialgleichungen usw. 40:28
- 01.2.1_2 Pfeile, Vektoren, gerichtete Größen 17:18
- 01.2.3 Ebene R2 und Raum R3 13:38
- 01.2.4 Vektorraum 16:01
!1 - 01.2.5 Basis, Dimension 20:51
!1!2 - 02.1 Geradengleichungen in Parameterform 15:09
- 02.2.1 Länge eines Vektors 10:28
- 02.2.2.1 Skalarprodukt, Teil 1 10:05
!1!2!3!4 - 02.2.2.2 Skalarprodukt Teil 2, Orthogonalität 24:49
- 03.1_2 Matrizen, Transposition, MATLAB(R) 21:59
- 03.3 Matrix mal Vektor, Matrix mal Matrix 23:05
!1 - 03.04_05_06 Skalierung, Drehungsmatrix, Verschiebung 29:40
- 04.01 Lineare Gleichungssysteme, Existenz und Eindeutigkeit von Lösungen 14:08
- 04.02 Existenz von Lösungen linearer Gleichungssysteme 14:43
- 04.03 Spaltenraum, Bild, Rang einer Matrix 18:51
!1!2 - 04.04 Eindeutigkeit der Lösung, homogenes Gleichungssystem 17:46
- 04.05 Kern, Defekt einer Matrix 12:25
- 04.06 Zeilenrang, Spaltenrang, unter-, überbestimmt 25:56
- 05.1.1 Determinate, Teil 1 14:42
!1 - 05.1.2 Determinante, Teil 2, Parallelepiped 18:25
- 05.1.3 Determinante, Teil 3, antisymmetrische Multilinearform 15:54
!1 - 05.1.4 Determinante, Teil 4, Entwickeln, Sarrus 28:23
- 05.2 Spatprodukt 3:54
- 05.3 Vektorprodukt rechnerisch 24:57
!1!2 - 05.4 Vektorprodukt geometrisch 22:45
- 05.5 Produkte mit Vektoren, Zusammenfassung 7:14
- 05.6 Inverse Matrix 15:18
- 06.1 Cramer-Verfahren 16:31
- 06.2 Gaußsches Eliminationsverfahren 20:48
- 06.3 Jacobi-Verfahren, iterative Lösung 12:45
!1!2 - 06.4 Lineare Gleichungssysteme mit MATLAB(R) und Wolfram Alpha 9:10
- 07.1 Eigenwerte, Eigenvektoren 11:12
- 07.2 Anwendungen von Eigenvektoren 16:51
- 07.3 Bestimmung von Eigenwerten 25:45
- 08.1_2 Dynamische Systeme, logistische Gleichung 26:59
- 08.3 Typen von Differentialgleichungen 18:06
- 08.4 Vektorfelder, Lösungskurven im Phasenraum 22:51
!1 - 09.1_2 Lösung durch Ansatz, homogene lineare DGL 1. Ordnung 13:00
- 09.3 inhomogene lineare DGL 1. Ordnung 13:44
- 09.4 Variation der Konstanten 9:22
- 09.5 homogene lineare DGL 2. Ordnung 32:04
- 09.6 inhomogene lineare DGL 2. Ordnung 9:16
- 10 Differentialgleichungen mit trennbaren Variablen 14:25
- 11.1 numerische Lösung von Differentialgleichungen 16:14
- 11.2_3 explizites, implizites Euler-Verfahren 20:22
- 11.4 symplektisches Verfahren 16:18
- 12.1 Differentialgleichungen höherer Ordnung 13:16
- 12.2 Differentialgleichungen in MATLAB(R) 6:35
!1!2!3 - 13.1 Differentialgleichungen mit Eigenvektoren lösen 29:41
!1!2 - 13.2 Exponentialfunktion von Matrizen 26:09
!1 - 13.2a Lösungsverfahren Differentialgleichungen 11:57
- 14.1 Tangentengerade, Schmiegeparabel, Taylor-Polynome 14:40
- 14.2 Taylor-Polynom für Wurzelfunktion 12:45
- 14.3.1 Taylor-Reihe, Potenzreihen, Teil 1 17:26
- 14.3.2 Taylor-Reihe, Potenzreihen, Teleskopsumme, Teil 2 19:41
- 15.1_2 Taylor-Rest, Teil 1 9:31
- 15.2.2_3 Taylor-Restformel, Teil 2, Abschätzung des Fehlers 28:47
!1 - 15.4 Taylor-Rest, Beispiel für Fehlerschätzung 8:55
- 15.5.1 Potenzreihen, Konvergenzradius, Teil 1 14:54
- 15.5.2 Konvergenzradius, Teil 2 18:07
!1 - 15.6 Potenzreihen und Analytische Funktionen 12:32
- 15.7 Differentialgleichungen mit Potenzreihen lösen 12:47
- 16.1 Fourier-Reihe, Spectrum Analyzer 18:32
!1 - 16.2 Raum der Funktionen mit Periode 1, Skalarprodukt, RMS 22:28
!1!2!3!4 - 16.3 komplexe Fourier-Reihe 24:33
- 16.4. Vollständigkeit der Fourier-Basis 6:26
- 16.5 komplexe Fourier-Reihe, beliebige Periode 11:53
- 17.1 Fourier-Reihe mit Sinus und Cosinus 12:16
!1 - 17.2 Fourier-Koeffizienten für Sinus und Cosinus 23:35
- 17.3 FFT in MATLAB(R), Window (Fensterfunktion), Hann 25:09
- 18.1_2 Kontinuierliche Fourier-Transformation, Satz von Plancherel 35:32
- 18.3 Laplace-Transformation 13:09
- 18.4 Laplace-Transformation von Ableitungen 11:50
- 18.5 Laplace-Transformation exp, cos, sin 15:00
- 18.6 Laplace-Transformation von Potenzfunktionen 7:39
- 18.7 Laplace-Transformation von verzögerten und zeitskalierten Funktionen 10:35
- 18.8 Fourier-, Laplace-, z-Transformation 4:23
- 19.1_2 Differentialgleichungen per Laplace-Transformation lösen 24:25
- 20.1_2 Funktionen mehrerer Veränderlicher, Höhenlinien, Kennlinienfeld, MATLAB(R) 32:35
!1 - 21.1 partielle Ableitung, Gradient, MATLAB(R) 27:03
- 21.2 Tangentialebene, Gradient, totales Differential 14:19
- 22.1 Fehlerfortpflanzung, Größtfehler 20:50
- 22.2 Fehlerfortpflanzung, Standardabweichung 25:04
!1 - 22.3 Extrema von Funktionen zweier Veränderlicher, Hesse-Matrix 31:18
!1!2!3 - 23.1_2 Polarkoordinaten 16:21
- 23.3 Zylinderkoordinaten 5:26
- 23.4 Kugelkoordinaten, geografische Länge und Breite 23:44
!1 - 24.1 Mehrdimensionale Integrale 15:12
- 24.2 Berechnung kartesischer Mehrfachintegrale 11:39
- 24.3 Integration in Polarkoordinaten, Kreisfläche 19:05
- 24.4 Integration in Kugelkoordinaten, Kugelvolumen 21:17
- 24.5 Kurvenintegral 9:21
Mathe 2, Sommer 2012
17:23:49
- 01A.1 Vektorraum, Untervektorraum, Basis, Dimension 32:02
!1!2 - 01A.2 Dimension von Kurven, Flächen; Hausdorff-Dimension; Fraktal, Koch-Kurve 25:30
- 02A.1 Probleme der Geradengleichung mx plus b 9:35
- 02A.2 Abstand Gerade vom Ursprung mit Ableitung und mit Normale 19:35
- 02A.3 Abstand Ebene vom Ursprung, aufwendige Form mit Ableitung 14:51
!1 - 02A.4 Abstand Ebene vom Ursprung, Normalform, Normalenvektor 19:24
- 02A.5 Boltzmann-Statistik per Skalarprodukt hergeleitet 38:13
!1 - 03A.1 Scherungsmatrix 6:16
- 03A.2 Rotation um beliebigen Punkt, affine Abbildung, Verschiebungsvektor, Rotationsmatrix 14:04
- 04A.1 Rang, Spaltenraum, Defekt, Kern einer Matrix, lineares Gleichungssystem 23:05
- 05A.1 Fläche eines Parallelogramms im R³, Vektorprodukt, Kreuzprodukt 8:43
- 05A.2 Vektorprodukt auflösbar oder nicht 3:02
- 05A.3 Trägheitstensor und Drehimpuls mit Vektorprodukt, Spatprodukt, Skalarprodukt 47:22
- 06A.1 Lineares Gleichungssystem, Gaußsches Eliminationsverfahren, Cramer-Regel, inverse Matrix 26:22
- 06A.2 mit Cramer-Regel 3×3-Matrix invertieren 10:43
- 06A.3 inverse Matrix eines Matrixprodukts 4:45
- 07A.1 Eigenwerte, Eigenvektoren bestimmen; charakteristisches Polynom 34:21
- 07A.2 Eigenwerte, Eigenvektoren symmetrischer Matrizen 10:21
- 08A.1 Differentialgleichungen klassifizieren, linear, homogen, konstante Koeffizienten, Ordnung 27:36
!1 - 08A.2 Schaltungssimulator im Browser, Circuit Lab 5:18
- 09A.1 Ladekurve Kondensator, inhomogene lineare Differentialgleichung 1. Ordnung 34:32
- 09A.2 homogene lineare Differentialgleichung 2. Ordnung, Spezialfall 6:36
!1 - 09A.3 vertikaler Wurf (senkrechter Wurf), inhomogene lineare Differentialgleichung 13:45
- 09A.4 Massenwirkungsgesetz, Differentialgleichungssystem 6:38
- 09A.5 Lotka-Volterra, Räuber-Beute-Modell, Differentialgleichungssystem 12:17
- 09A.6 Differentialgleichung mit Randbedingungen; quantenmechanisches Teilchen im Potentialtopf 11:04
- 10A.1 Differentialgleichung mit trennbaren Variablen, Beispiel 5:03
- 10A.2 logistische Differentialgleichung, Differentialgleichung mit trennbaren Variablen 25:39
!1 - 11A.1 Lotka-Volterra, Differentialgleichung numerisch lösen, Räuber-Beute 17:09
!1 - 11A.2 Stabilität von Differentialgleichungslösern, A-Stabilität, explizites Euler-Verfahren 13:16
- 12A.1 homogene Differentialgleichung vierter Ordnung 8:59
- 12A.2 Differentialgleichung höherer Ordnung in DGL-System erster Ordnung umwandeln 6:45
- 13A.1 lineare Differentialgleichung als DGL-System mit Eigenwerten und Eigenvektoren lösen 20:19
- 13A.2 Rotationsmatrix in 3D per Differentialgleichungssystem, Exponentialfunktion von Matrizen 16:39
!1 - 14A.1 kubische Wurzel mit Schmiegeparabel nähern, Taylor-Polynom 16:21
- 14A.2 nichtlineare Gleichung mit Schmiegeparabel in quadr. Gleichung umwandeln, Taylor 12:14
- 14A.3 Divergenz der harmonischen Reihe mit Integral zeigen 6:56
- 15A.1 Potenzreihe für Arcustangens; Konvergenzradius 42:46
!1 - 16A.1 Jede (übliche) periodische Funktion lässt sich als Fourier-Reihe schreiben; Delta-Funktion 26:48
- 16A.2 Vektorraum von Funktionen, Norm, Skalarprodukt, Vorbereitung Fourier-Reihe 9:06
- 16A.3 Fourier-Reihe als Zerlegung von Vektoren; Orthonormalbasis, Skalarprodukt 26:15
- 17A.1 Fourier-Reihe einer Rechteckschwingung 25:28
!1!2 - 17A.2 Formel für pi aus Fourier-Reihe einer Rechteckschwingung 7:37
!1!2 - 17A.3 Fourier-Reihe Dreiecksschwingung; noch eine Formel für pi 16:08
- 17A.4 Fourier-Reihe Sägezahn mittels Rechteck 14:54
- 18A.1 Laplace-Transformation von t mal y(t) 13:34
- 19A.1 Differentialgleichung per Laplace-Transformation lösen 12:03
- 19A.2 noch eine Differentialgleichung per Laplace-Transformation lösen 19:54
- 20A.1 Funktionsplot in 3D mit Google 3:08
- 20A.2 Eierkartonfläche sin(x)sin(y) in 3D zeichnen 13:07
- 20A.3 Gleichung des idealen Gases plotten, 3D, Höhenlinien, Kennlinienfeld 24:42
- 20A.4 Allgemeine Potenzfunktion x^y in 3D plotten; Stetigkeit 5:38
- 21A.1 Beispiel Höhenlinien, Gradient, partielle Ableitung 13:29
- 21A.2 Beispiel 2 Höhenlinien, Gradient, partielle Ableitung 9:39
- 21A.3 totales Differential, Tangentialebene, ideales Gasgesetz 19:07
- 22A.1 Fehlerfortpflanzung, Größtfehler, Funktion zweier Veränderlicher 18:30
!1!2 - 22A.2 Fehlerfortfplanzung, Standardabweichung, Funktion zweier Veränderlicher 16:37
- 22A.3 lokale Maxima, Minima einer Funktion zweier Veränderlicher; Hesse-Matrix 19:24
- 22A.4 nochmal lokale Maxima, Minima einer Funktion zweier Veränderlicher; Hesse-Matrix 15:36
!1 - 22A.5 Kriterium für positive Eigenwerte der 2×2-Hesse-Matrix 10:37
!1 - 22A.6 Globales Maximum einer Funktion von zwei Veränderlichen; Werte am Rand 10:44
!1 - 24A.1 Beispiel Doppelintegral, Volumen zwischen Funktionsfläche und Dreieck 10:20
- 24A.2 Volumen unter Paraboloid, Doppelintegral in Polarkoordinaten 13:51
- 24A.3 Fläche unter Gauß-Glocke; Normalverteilung; Doppelintegral in Polarkoordinaten 9:27
Mathe 2, Sommer 2013
23:03:33
- 01B.1 Begriff Vektorraum; Vektor aus zwei gegebenen Vektoren bilden 10:29
- 01B.2 Vektorraum der Polynome; Basis 17:04
- 01B.3 Vektorraum der sinusförmigen Schwingungen; Zerlegung in sin und cos 9:26
- 02B.1 Geraden auf Parallelität prüfen 4:25
- 02B.2 Schnittpunkt zweier Geraden 11:27
!1 - 02B.3 prüfen, ob Ebene durch Ursprung geht 8:54
- 02B.4 Schnittmenge Ebene mit xy-Ebene 3:19
- 02B.5 Winkel mittels Skalarprodukt bestimmen 5:33
- 02B.6 Dreieck auf Rechtwinkligkeit prüfen 5:20
- 02B.7 Vektor in yz-Ebene senkrecht zu gegebenem Vektor 7:48
- 02B.8 Geradengleichung in Normalenform 12:09
!1 - 02B.9 Parallelogrammidentität; Diagonalen eines Parallelogramms 9:56
- 02B.10 Winkel zwischen zwei Geraden im R² 5:50
- 03B.1 geometrische Wirkung einer Matrix; inverse Matrix 17:54
- 03B.2 Spiegelung und Drehung nacheinander; Matrizenmultiplikation 7:20
- 03B.3 Nichtkommutativität des Matrizenprodukts 9:03
- 03B.4 zwei Spiegelungen nacheinander; Reihenfolge; Matrizenmultiplikation 12:12
- 03B.5 achte Potenz einer Matrix; Matrizen und komplexe Zahlen 8:44
!1 - 03B.7 dritte Potenz einer Matrix soll die Einheitsmatrix sein 3:30
- 03B.8 Spiegelungsmatrix aus Spiegelungsachse berechnen 11:46
- 03B.9 Spiegelungsachse aus Punkt und Bild bestimmen 5:20
- 03B.10 Matrix für Drehung um Hauptdiagonale im Raum 5:44
- 03B.11 Rezept für Matrizenprodukt 2:33
- 04B.1 Lineare Gleichungssysteme; Lösungen nicht existent oder nicht eindeutig 9:40
- 04B.2 Spaltenraum, Rang, Defekt einer 2×3-Matrix 21:17
!1 - 04B.3 Matrix zu gegebenem Spaltenraum finden 2:46
!1 - 04B.4 Matrix mit Rang 3 mal Matrix mit Rang 1 soll Nullmatrix sein 13:26
- 04B.5 Beispiel Spaltenraum, Bild, Rang, Kern, Defekt; lineares Gleichungssystem 23:03
- 04B.6 weiteres Beispiel Spaltenraum, Bild, Rang, Kern, Defekt; lineares Gleichungssystem 12:11
- 05B.1 Fläche eines Parallelograms im R² mittels Determinante 5:40
- 05B.2 eine 3×3-Determinante ausrechnen 5:06
- 05B.3 eine 4×4-Determinante ausrechnen 14:01
- 05B.4 Fläche eines Dreiecks im Raum 10:25
- 05B.5 Vektorprodukt gleich gegebenem Vektor 4:29
- 05B.6 Gerade senkrecht durch Ebene; Abstand Ebene von Ursprung 13:19
- 05B.7 Vektor senkrecht zu drei gegebenen im R^4 6:25
- 05B.8 doppeltes Vektorprodukt; BAC-CAB-Formel 12:40
- 06B.1 inverse Matrix einer 2×2-Matrix; Gleichungssystem lösen 15:45
- 06B.2 vier Lösungsverfahren für lineare Gleichungssysteme; Cramer, Gauß, Jacobi, inverse Matrix 29:15
!1 - 06B.3 Gleichungssystem 2×3; Gaußsches Eliminationsverfahren; Bild, Rang, Kern, Defekt 22:07
!1 - 07B.1 Eigenwerte einer 3×3-Matrix 15:07
- 07B.2 Eigenvektoren von 2×2- und 3×3-Matrizen bestimmen 14:37
- 07B.3 Matrix zu Eigenvektor und Eigenwert bestimmen 5:22
!1 - 07B.4 Eigenwerte einer 2×2-Drehungsmatrix 2:03
- 07B.5 Eigenwerte und Eigenvektoren einer 3×3-Matrix 23:15
!1!2 - 07B.6 Eigenwerte mit Spur und Determinante prüfen 8:32
!1!2 - 07B.7 Eigenwerte einer 3×3-Matrix; Test mit Spur und Determinante 5:39
- 07B.8 Eigenvektor zu einer 3×3-Matrix; Eigenwert gegeben 11:36
!1 - 07B.9 Eigenwerte, Eigenvektoren einer 2×2-Matrix 9:06
- 08B.1 SIR-Modell für Infektionsausbreitung; Differentialgleichungen 30:15
!1!2 - 09B.1 lineare Differentialgleichungen; Begriffe; Beispiel 15:47
- 09B.2 homogene lineare Differentialgleichung mit konstanten Koeffizienten 7:08
- 09B.3 inhomogene lineare Differentialgleichung mit konstanten Koeffizienten 15:42
- 09B.4 inhomogene lineare Differentialgleichung; Sonderfall 3:10
- 09B.5 inhomogene lineare Differentialgleichung; Anfangsbedingungen 16:00
!1 - 09B.6 inhomogene lineare Differentialgleichung, Sonderfall 9:01
!1 - 09B.7 inhomogene lineare Differentialgleichung 3. Ordnung 3:10
- 09B.8 inhomogene lineare Differentialgleichung; Verhalten im Unendlichen 14:51
!1 - 09B.9 Baumwachstum mit Differentialgleichung simulieren; nichtlineare DGL 16:57
- 10B.1 Differentialgleichung zum Üben 9:57
- 10B.2 Differentialgleichung zum Üben 10:01
- 10B.3 Differentialgleichung zum Üben 2:27
- 10B.4 Differentialgleichung zum Üben 5:17
- 10B.5 Differentialgleichung zum Üben 19:09
- 10B.6 Differentialgleichung zum Üben; Abklingen oder Anwachsen 3:22
!1 - 10B.7 Differentialgleichung zum Üben; Abklingen oder Anwachsen 6:08
- 10B.8 Differentialgleichung zum Üben 7:27
- 10B.9 Differentialgleichung zum Üben 6:55
- 10B.10 Differentialgleichung zum Üben; Abklingen oder Anwachsen 5:16
!1!2!3!4 - 10B.11 Differentialgleichung zum Üben 7:14
- 10B.12 Differentialgleichung zum Üben 5:58
- 10B.13 Differentialgleichung zum Üben 7:11
- 10B.14 Differentialgleichung zum Üben 3:14
- 10B.15 Klassifikation von Differentialgleichungen 14:53
!1 - 10B.16 Differentialgleichung zum Üben 11:53
!1 - 10B.17 Differentialgleichung zum Üben 6:42
- 11B.1 Satellitenorbit; Euler-Verfahren, numerische Lösung von Differentialgleichungen 25:23
!1!2!3 - 12B.1 Differentialgleichung 3. Ordnung in DGL-System 1. Ordnung umwandeln 6:44
!1 - 13B.1 Exponentialfunktion von Matrix; Differentialgleichungssystem dazu 18:13
- 13B.2 lineares Differentialgleichungssystem mit Vektoren lösen 10:38
- 13B.3 homogene lineare Differentialgleichung 2. Ordnung mittels Matrix lösen 6:57
- 14B.1 Taylor-Näherung für natürlichen Logarithmus 10:25
- 15B.1 Taylor-Näherung und Fehler für Sinusfunktion 17:20
- 15B.2 Potenzreihe für Logarithmus aus geometrischer Reihe 4:55
!1!2 - 15B.3 Potenzreihenansatz für Differentialgleichung; Beispiel Taylorpolynom 13:26
- 15B.4 Potenzreihenansatz für Differentialgleichung 19:14
- 15B.5 kubische Wurzel mit Taylorpolynom schätzen; Fehlerschranke 10:34
!1!2!3 - 16B.1 Beispiel Fourier-Reihe; Bedeutung 41:00
!1!2 - 16B.2 Sinusförmige Wechselspannung, Effektivwert 9:35
!1!2 - 16B.3 komplexe Fourier-Reihe für Sinus; Effektivwert 24:35
- 16B.4 komplexe Fourier-Reihe für dreiecksförmige Schwingung 12:18
!1!2!3!4 - 16B.5 Sägezahnschwingung; Mittelwert, Effektivwert 10:04
- 16B.6 Fourier-Reihe für verschobene und skalierte Funktion 16:03
- 17B.1 Fourier-Reihe mit Cosinus und Sinus für dreiecksförmige Schwingung 12:08
!1 - 17B.2 Fourier-Reihe mit Cosinus und Sinus für rechteckförmige Schwingung; Effektivwert 15:42
!1 - 17B.3 Fourier-Reihe mit Cosinus und Sinus für verschobenen Sinus 8:44
- 17B.4 Fourier-Reihe mit Cosinus und Sinus für asymmetrische Rechteckschwingung 13:48
- 18B.1 Laplace-Transformierte einer Rampe 10:59
- 18B.2 Laplace-Transformierte einer eingeschalteten sinusförmigen Schwingung 16:42
- 18B.3 Grenzwert von s mal Laplace-Transformierte 6:55
- 18B.4 inverse Laplace-Transformation per Partialbruchzerlegung; Beispiel 9:17
- 18B.5 inverse Laplace-Transformation per Partialbruchzerlegung, Beispiel 11:02
- 19B.1 Differentialgleichung per Laplace-Transformation lösen 18:27
!1 - 20B.1 sin(xy) plotten in 3D, mit Höhenlinien und als Kennlinienfeld 21:56
- 21B.1 Beispiel partielle Ableitungen, Gradient; Anschauung 14:35
- 21B.2 weiteres Beispiel Höhenlinien, Gradient; Anschauung 12:57
- 21B.3 Beispiel Gradient in 2D und 3D; Äquipotentialflächen 29:34
- 21B.4 Beispiel lineare Näherung in zwei Veränderlichen; Tangentialebene 11:37
- 21B.5 Beispiel lineare Näherung in zwei Veränderlichen; Tangentialebene; totales Differential 7:06
- 21B.6 maximale Windenergieausbeute; Tangentialebene; lineare Näherung 13:48
!1 - 22B.1 lokale Minima, Maxima bei zwei Veränderlichen; Beispiel 21:12
- 23B.1 Funktion in Polarkoordinaten bzw. kartesischen Koordinaten 6:37
- 23B.2 Ellipse in Polarkoordinaten und kartesischen Koordinaten 18:22
- 23B.3 Ebene in sphärischen Koordinaten 14:58
- 23B.4 Gradient in Polarkoordinaten 20:41
- 24B.1 Beispiel Doppelintegral 17:15
- 24B.2 Doppelintegral in Polarkoordinaten und kartesischen Koordinaten 14:04
Mathe 2, Sommer 2014
20:47:09
- 01C.1 Lieferwagen mittels Vektorrechnung füllen 19:38
- 01C.2 Ausgleichskurve mittels Vektorrechnung 39:21
!1 - 01C.3 Vektor im R³ in zwei zueinander senkrechte Anteile zerlegen 15:49
- 03C.1 zwei Matrizen, deren Produkt die Nullmatrix ist 6:54
- 03C.2 Rotationen um 90° im R³ um Koordinatenachsen; mehrere hintereinander 16:52
- 03C.3 Matrix für Spiegelung an Ebene im R³ 9:53
- 04C.1 Spaltenraum = Bild, Rang, lineares Gleichungssystem an Beispielen 40:29
- 04C.2 Bild, Rang, Kern, Defekt einer Matrix; lineares Gleichungssystem 19:56
- 04C.3 unterbestimmtes LGS ohne Lösung; überbestimmtes LGS nicht eindeutig lösbar 8:49
- 04C.4 Rang, Spaltenraum (Bild), Defekt, Kern einer Matrix an Beispielen 21:25
- 04C.5 Matrix zu gegebenem Kern 3:48
- 04C.6 lineares Gleichungssystem zu gegebener Lösungsmenge 10:59
- 05C.1 mögliche Werte für Rang, Defekt, Determinante 17:57
- 05C.2 Determinanten zu Null machen 15:08
- 05C.3 Vektorprodukt im Vierdimensionalen 13:16
- 06C.1 Begründung für Cramersche Regel 11:18
- 06C.2 Cramersche Regel schlägt fehl; Gaußsche Elimination 16:27
- 06C.3 2×2-Gleichungssystem mit inverser Matrix lösen 6:20
- 07C.1 Eigenwerte, Eigenvektoren einer 3×3- und einer 4×4-Matrix 40:00
!1!2 - 07C.2 Eigenwerte und Eigenvektoren von Spiegelung und Drehungen im R² und im R³ 20:21
- 08C.1 sieben einfache Differentialgleichungen 29:39
- 08C.2 Differentialgleichung für Widerstand und Kondensator an Netzspannung 26:47
- 08C.3 komplexe Widerstände statt Differentialgleichungen 43:11
- 09C.1 inhomogene lineare Differentialgleichung 1. Ordnung mit konstanten Koeffizienten 19:54
- 09C.2 inhomogene lineare Differentialgleichung 2. Ordnung mit konstanten Koeffizienten 16:19
!1!2 - 10C.1 zwei Differentialgleichungen zum Üben 23:11
- 10C.2 zwei Differentialgleichungen zum Üben 7:35
- 10C.3 vier Differentialgleichungen zum Üben 31:27
!1 - 10C.4 Differentialgleichung zum Üben; reelle und komplexe Lösungen 17:47
- 11C.1 Widerstand und Kondensator an Netzspannung analytisch und numerisch 45:09
- 11C.2 einfacher Gleichrichter; numerische Lösung der Differentialgleichung 36:52
!1!2 - 12C.1 Differentialgleichung dritter Ordnung in Differentialgleichungssystem erster Ordnung umwandeln 9:24
!1!2 - 14C.1 Wurzeln mit Taylorpolynomen nähern 16:16
!1!2 - 14C.2 klassische kinetische Energie als Näherung der Relativitätstheorie 7:50
!1 - 14C.3 Logarithmus direkt und indirekt über Schmiegeparabel schätzen 12:14
!1!2 - 14C.4 Gaußglocke integrieren mittels Näherung vierter Ordnung 11:20
- 14C.5 Feld eines elektrischen Dipols mittels linearer Näherung 12:25
- 14C.6 Taylor-Polynom für Produkt zweier Funktionen 15:38
- 15C.1 Taylor-Rest mit partieller Integration herleiten 11:40
- 15C.2 Differentialgleichung mit Potenzreihenansatz knacken 7:47
!1 - 16C.1 Beispiel für Fourier-Analyse im Komplexen 39:10
- 16C.2 Phasenanschnitt; Effektivwert und komplexe Fourier-Reihe, Teil 1 39:49
!1!2 - 16C.3 Phasenanschnitt, komplexe Fourier-Reihe, Teil 2 33:28
- 17C.1 Phasenanschnitt; komplexe und reelle Fourier-Reihe, Teil 3 22:23
- 17C.2 reelle Fourier-Koeffizienten und Symmetrie 7:06
!1 - 17C.3 Kurzfassung Fourier-Reihe, reell und komplex 29:13
- 18C.1 Laplace-Transformation von ein, zwei, drei, unendlich vielen Zacken 29:55
- 19C.1 Differentialgleichungen per Laplace-Transformation lösen 34:24
!1!2 - 20C.1 Ohmsches Gesetz als 3D-Fläche, mit Höhenlinien und als Kennlinienfeld 30:08
- 21C.1 elektrisches Feld und Gradient des Potenzials; Punktladung 32:19
!1!2!3!4!5!6 - 22C.1 Beispiel Größtfehler und Standardabweichung bei zwei Veränderlichen 20:21
- 22C.2 lokale Minima und Maxima einer Funktion zweier Veränderlicher 10:29
!1!2 - 22C.3 lokale Minima und Maxima noch einer Funktion zweier Veränderlicher 12:04
!1!2 - 22C.4 lokales Extremum einer Funktion dreier Veränderlicher 13:10
!1!2!3 - 22C.5 Lokales Maximum oder Minimum einer Funktion zweier Veränderlicher 12:31
!1 - 23C.1 Länge Luftlinie Bielefeld-Hamburg mit sphärischen Koordinaten 35:58
!1 - 23C.2 Kurs Bielefeld-Hamburg mit sphärischen Koordinaten 30:51
!1!2 - 24C.1 Volumen zwischen Dreieck und Paraboloid; Doppelintegral 15:35
- 24C.2 Flächeninhalt einer Schnecke; Polarkoordinaten 11:45
!1 - 24C.3 Volumen eines Kegelstumpfs mit Dreifachintegral und Zylinderkoordinaten 29:25
Mathe 2, Sommer 2015
18:42:17
- 01D.1 Vektorrechnung, Länge, Dimension 36:28
- 01D.2 Vektorrechnung, Basis 19:05
- 01D.3 Funktionen als Vektoren verstehen 12:38
- 01D.4 drehbare Feder per Vektorrechnung; Software für Vektorrechnung 30:33
- 03D.1 einige Produkte Matrix mal Vektor, Matrix mal Matrix; Transposition 18:35
- 03D.2 Matrizen für eine Spiegelung im R² und eine Drehung im R³ 15:22
- 03D.3 Matrix und Verschiebungsvektor für Drehung im R² 17:39
!1 - 03D.4 Matrix und Verschiebungsvektor für Spiegelung im R³ 17:14
- 04D.1 lineares Gleichungssystem, Lösungsmenge, Koeffizientenmatrix, Rang usw. 36:44
- 05D.1 Idee der Determinante, Beispiele 2×2, 3×3, 4×4 43:10
!1 - 05D.2 Determinante, Rang, Defekt 9:40
- 05D.3 Fläche eines Parallelogramms im R³; Vektorprodukt 14:02
- 05D.4 Fläche eines Parallelogramms in R²; Determinante 15:07
- 05D.5 Kern einer 3×3-Matrix mittels Vektorprodukt 11:24
- 06D.1 Cramer-Verfahren am Beispiel; Begründung 18:39
- 06D.2 Cramer-Verfahren 4×4; Software 9:57
- 06D.3 Gaußsches Eliminationsverfahren am Beispiel 11:37
!1 - 08D.1 einige einfache Differentialgleichungen 22:45
- 08D.2 Schleppkurve (Traktrix); Differentialgleichung aufstellen 10:20
- 09D.1 lineare Differentialgleichung 2. Ordnung, zwei Spezialfälle 59:25
!1!2!3!4 - 09D.2 komplexe Exponenten bei linearer Differentialgleichung 2. Ordnung 10:35
- 09D.3 Differentialgleichung mit Lösungen e^x und e^-x 3:37
- 10D.1 Differentialgleichung zum Üben 6:46
- 11D.1 Van-der-Pol-Differentialgleichung und harmonischer Oszillator 42:41
!1 - 12D.1 eine Differentialgleichung 3. Ordnung 17:26
!1 - 12D.2 eine Differentialgleichung 4. Ordnung 8:06
- 13D.1 zweimal Kondensator und Widerstand, Differentialgleichungssystem; Teil 1 29:38
!1!2 - 13D.2 zweimal Kondensator und Widerstand, Differentialgleichungssystem; Teil 2 22:47
- 14D.1 Kehrwert der Wurzel(4,01) mit Taylor schätzen 14:19
- 14D.2 Logarithmus ins Quadrat mit Taylor nähern 5:12
- 14D.3 mit Taylor e^x = 100 x näherungsweise lösen 28:03
!1!2 - 14D.4 mit Taylor x^x = 5 näherungsweise lösen 12:20
!1 - 15D.1 Potenzreihenansatz für Van-der-Pol-Differentialgleichung 25:57
- 15D.2 Potenzreihe für 1 durch 3+x², Konvergenzradius 14:54
- 16D.1 Fourier-Reihe als Zerlegung in Basisvektoren 48:49
!1 - 16D.2 Beispiel komplexe Fourier-Koeffizienten, Effektivwert 35:15
- 17D.1 reelle und komplexe Fourier-Reihe im Vergleich 35:52
- 17D.2 einfache Beispielrechnung für reelle Fourier-Koeffizienten 7:47
- 17D.3 zwei reelle Fourier-Koeffizienten einer Dreiecksschwingung 22:48
!1!2 - 17D.4 Fourier-Koeffizienten der Einweg-gleichgerichteten Sinusschwingung 15:38
- 18D.1 Laplace-Transformation allgemein und von abgeschnittener Exponentialfunktion 22:08
- 18D.2 Laplace-Transformation von abgeschnittenem Sinus 9:29
- 18D.3 Laplace-Transformation von Integral 6:10
- 19D.1 Differentialgleichung per Laplace-Transformation und per Ansatz lösen 29:03
- 19D.2 noch eine Differentialgleichung per Laplace-Transformation und per Ansatz lösen; Sonderfall 10:33
- 19D.3 Lage der Polstellen der Laplace-Transformierten 18:40
- 20D.1 Höhenlinien und Gesamtverlauf von e^(x² durch y) als Funktion zweier Veränderlicher 32:12
- 21D.1 Beispiele für partielle Ableitungen 9:10
!1 - 21D.2 Eierkartonfläche, Höhenlinien, Gradient 24:13
- 21D.3 Funktion zu vier Gradientenvektoren, Sattel, hyperbolisches Paraboloid 11:08
- 21D.4 lineare Näherung einer Funktion mit zwei Veränderlichen; totales Differential 9:09
- 21D.5 Tangentialebene an Funktion zweier Veränderlicher; Normalenform 17:51
- 21D.6 quadratische Funktion zu gegebener Tangentialebene finden 9:33
!1 - 22D.1 Fehlerrechnung für Volumen einer Dose 32:09
- 22D.2 Beispiel für lokale Minima, Maxima einer Funktion zweier Veränderlicher 6:45
- 23D.1 Kardioide in Polarkoordinaten 35:10
Mathe 2, Sommer 2016
15:35:18
- 01E.1 Linearkombinationen von Pfeilen und von Funktionen 43:14
- W01 komplexe Zahlen in Polarform umwandeln 6:52
- W02 Sinus und Cosinus vom dreifachen Winkel 9:12
- W03 Mischung von Sinus und Cosinus 9:48
- 02E.1 lineare Abbildungen von geometrischen Vektoren und von Funktionen 23:13
!1 - 02E.2 Ebenengleichung aufstellen und prüfen, ob der Ursprung enthalten ist 6:56
- 03E.1 Kettenmatrix für ein einfaches Zweitor aufstellen 7:45
- 04E.1 Beispiele für die Lösbarkeit linearer Gleichungssysteme; Bild, Rang, Kern, Defekt 39:23
!1 - 04E.2 Matrix zu gegebenem Spaltenraum finden 13:33
- 04E.3 Matrix zu gegebenem Kern finden 15:59
- 04E.4 Spiegelungs- und Drehungsmatrix bestimmen; Hintereinanderausführung; lineare Gleichungssysteme 28:39
!1 - 04E.5 Reaktionsgleichung mit linearem Gleichungssystem ausbalancieren 27:45
- 05E.1 Determinanten von zwei 3×3-Matrizen und deren Produkt; Dreiecksmatrix 19:51
- 05E.2 Beispiel für Entwicklung einer 4×4-Determinante 3:06
- 05E.3 Matrix für senkrechte Projektion; davon Bild, Rang, Kern, Defekt, Determinante, Quadrat 13:22
!1 - 06E.1 Gaußsches Eliminationsverfahren am Beispiel; Sonderfälle 19:47
!1!2 - 06E.2 Cramer-Verfahren am Beispiel 13:03
- 07E.1 Matrix aus Eigenvektoren und Eigenwerten bestimmen 13:05
- 07E.2 Idee hinter Google PageRank, Übergangsmatrix, Eigenwert 1 23:27
- 07E.3 Eigenwerte von Spiegelungsmatrizen und von 5×5-Matrix mit Rang 2 5:49
- 07E.4 Eigenwerte und Eigenvektoren einer 2×2-Matrix, Beispiel 5:50
- 07E.5 Eintrag in 2×2-Matrix so wählen, dass Eigenwerte reell 4:59
- 08E.1 einige einfache Differentialgleichungen zum Einstieg 22:06
!1!2 - 08E.2 Michaelis-Menten-Kinetik, Differentialgleichungssystem 24:19
!1 - 09E.1 gedämpfter elektrischer Schwingkreis; Differentialgleichung 21:16
- 10E.1 Differentialgleichung zum Üben 14:12
- 10E.2 Differentialgleichung zum Üben 13:47
- 10E.3 Differentialgleichung zum Üben 13:40
- 10E.4 Differentialgleichung zum Üben 3:56
- 10E.5 Differentialgleichung zum Üben 5:51
- 10E.6 Festellen, ob jede Lösung der Differentialgleichung abklingt 5:44
- 10E.7 Differentialgleichung zum Üben 3:49
- 10E.8 logarithmische Übertemperatur; Differentialgleichung für Heizkörper 28:28
- 10E.9 Differentialgleichung zum Üben 6:43
!1 - 11E.1 Dahlquist-Testdifferentialgleichung, explizites und implizites Euler-Verfahren 29:46
- 12E.1 Differentialgleichung dritter Ordnung mit Euler-Verfahren lösen 16:50
!1 - 13E.1 homogenes lineares Differentialgleichungssystem mittels Eigenwerten und Eigenvektoren lösen 16:25
!1 - 13E.2 inhomogenes lineares Differentialgleichungssystem lösen 11:58
- 14E.1 kubische Näherung des Kehrwerts der dritten Wurzel von 8,01 14:31
- 14E.2 quadratische Näherung von Wurzel(cos(0,01)) 9:13
- 15E.1 Potenzeihe für 2^x, Taylor-Polynom, Fehlerschätzung 32:15
- 15E.2 Potenzreihenansatz für die Differentialgleichung y‘ = y² + sin(x) 21:57
- 18E.1 Abtasttheorem, sinc 39:19
- 18E.2 Fourier- und Laplace-Transformation eines Pulses 21:30
- 18E.3 Laplace-Transformation von Exponentialfunktion mal Signal 5:26
- 18E.4 Laplace-Transformation von Cosinus mal Signal 3:07
- 18E.5 Beispiel für Laplace-Rücktransformation 28:16
- 21E.1 Rechenbeispiel zu partiellen Ableitungen 6:05
- 21E.2 Beispiel zu partiellen Ableitungen, Gradient, lineare Näherung, Tangentialebene 21:37
!1!2 - 21E.3 totales Differential und lineare Näherung für Masse einer Kugel; wozu lineare Näherung 11:57
- 21E.4 Gradient von 1 durch r 4:48
- 21E.5 totales Differential eines Winkels im rechtwinkligen Dreieck 7:59
- 22E.1 lokales Extremum einer Funktion zweier Veränderlicher; Kriterium am Beispiel 16:57
- 22E.2 lokale Minima einer Funktion zweier Veränderlicher suchen 6:23
- 22E.3 Funktion zweier Veränderlicher hinschreiben, die einen Sattel hat 2:55
- 22E.4 quadratische Näherung einer Funktion zweier Veränderlicher; Beispiel 1,02 hoch 3,04 20:56
- 23E.1 drei Beispielfiguren in Polarkoordinaten 13:04
!1 - 23E.2 ein Kegel in kartesischen, Zylinder- und Kugel-Koordinaten 4:03
- 23E.3 ein Zylinder in kartesischen, Zylinder- und Kugel-Koordinaten 3:39
!1 - 23E.4 Satz des Pythagoras auf der Kugel 21:37
!1!2!3!4!5 - 24E.1 Integrale über zwei Veränderliche in Polarkoordinaten, am Beispiel sin(x²+y²) 24:16
!1
Mathe 2, Sommer 2017
11:09:20
- 01F.1 Vektoren im Dreieck, Seitenmitten, Schwerpunkt 15:17
- 01F.2 Datenreihen und Funktionen als Vektoren 8:46
- 01F.3 Basen des R²; ein Unterraum des R³ 8:02
- 02F.1 Gerade im R³; Abstand eines Punkts davon 28:53
- 03F.1 einige Matrizen und Vektoren multiplizieren 8:29
- 03F.2 Drehungsmatrix geometrisch und mittels komplexer Zahlen 23:25
- 04F.1 Beispiel für Bild, Rang, Kern, Defekt einer Matrix 34:40
- 05F.1 Determinante; Bedeutung und Grundregeln 29:02
- 05F.3 Eigenschaften von Skalarprodukt, Vektorprodukt, Spatprodukt 18:47
- 05F.4 inverse Matrix einer 2×2-Matrix 5:54
- 07F.1 Eigenwert, Eigenvektor; Wiederholung Rang, Defekt, Determinante 16:26
- 07F.2 Lineare Algebra am Beispiel einer Spiegelungsmatrix wiederholt 24:42
- 09F.1 Beispiele für lineare Differentialgleichungen 1. Ordnung 33:32
- 09F.2 lineare Differentialgleichung 2. Ordnung mit konstanten Koeffizienten 13:14
- 10F.1 weitere Beispiele für lineare Differentialgleichungen 1. Ordnung 31:22
- 13F.1 Übersicht zu Lösungsverfahren für Differentialgleichungen 17:58
- 15F.1 Taylor-Polynom und Rest am Beispiel kubische Wurzel aus 8,01 35:02
- 15F.2 Taylor-Reihe für arctan; Reihe für Pi 15:51
- 16F.1 komplexe Fourier-Koeffizienten am Beispiel einer rechteckförmigen Schwingung 31:26
- 17F.1 Fourier-Reihe für Sägezahn und Rechteck aus Dirac-Kamm 40:31
- 17F.2 Pi und Fourier-Reihe für Dreieckschwingung aus Rechteckschwingung 11:49
- 18F.1 Fourier- und Laplace-Transformation eines an- und abgeschalteten Sinus 33:09
- 18F.2 inverse Laplace-Transformation per Partialbruchzerlegung; Beispiel 13:33
- 19F.1 lineare Differentialgleichung lösen mit und ohne Laplace-Transformation 25:17
- 19F.2 Laplace-Transformationen der Grundfunktionen mittels Differentialgleichungen hergeleitet 13:03
- 21F.1 Softmax-Funktion als Beispiel für Höhenlinien, Isoflächen, Gradient 34:03
- 21F.2 Gradient Descent zur numerischen Minimierung 21:33
- 22F.1 lokales Extremum einer Funktion zweier Veränderlicher; Kriterien; Taylor-Näherung 23:58
- 22F.2 lokales Extremum einer Funktion zweier Veränderlicher, weiteres Beispiel 6:31
- 23F.1 Laplace-Operator in Polarkoordinaten; Wärmeleitung 45:05
Mathe-Vorkurs 2013
8:26:29
- 001 Grundrechenarten, Teilen durch Null 6:55
- 002 Ausmultiplizieren, Klammern, Rechnen mit Buchstaben 7:55
- 003_004 erste, zweite, kubische binomische Formel; minus mal minus 12:45
- 005 Binomische Formeln geometrisch 3:45
- 006 Dritte binomische Formel 1:22
- 007 Brüche 4:29
- 008 Erweitern und Kürzen 3:54
- 009 Brüche multiplizieren, Doppelbrüche 6:52
- 010 Brüche addieren, Hauptnenner 3:26
- 011 Dezimalbrüche 3:50
- 012 Umformen, Auflösen 4:47
- 013 Brüche auflösen, Definitionsmenge 2:42
- 013a (015) Definitionsmenge von Ausdrücken 7:12
- 014 Produkt ist null 8:16
- 020 Summenzeichen, Produktzeichen 2:53
- 021 Proportionalität 6:59
- 022 Proportionalität, Einheiten 4:01
- 023 Ursprungsgeraden, Steigung 5:31
- 024 Dreisatz 3:33
- 027 Lineare Funktionen, Achsenabschnitt 5:50
- 028 weiter lineare Funktionen 3:34
!1 - 029 Stückweise definierte Funktionen 4:05
!1!2!3!4 - 030 Absolutbetrag 2:43
- 031 Ganzzahlige positive Potenzen 5:43
!1 - 032 Potenzen; Summen und Differenzen im Exponenten 5:09
- 033 Nullte und erste Potenz; null hoch eins; null hoch null 6:00
- 034 Negative Potenzen 5:02
- 035 Gebrochenzahlige Potenzen 6:27
- 036 Wurzeln 3:45
!1!2 - 037 Wurzeln von Produkten, Quotienten, Summen 1:41
- 038 Exponentialdarstellung von Dezimalzahlen 4:45
- 039 Potenzfunktionen und Exponentialfunktionen 6:21
!1 - 040 Exponentielles Wachstum 7:01
- 041 Exponentieller Zerfall 3:39
!1 - 041a Natürliche Exponentialfunktion, Eulersche Zahl 3:04
!1!2 - 042 Logarithmen 7:24
- 043 Rechenregeln für Logarithmen 6:19
- 044 Logarithmen zu fremden Basen 5:13
- 045 Verkettete Funktionen, af(x)+b 5:46
- 046 Verkettete Funktionen, f(ax+b) 5:25
- 047 Bogenmaß 6:55
- 048 Dreieck; Summe der Innenwinkel 3:50
- 049 Fläche eines Dreiecks 1:58
- 050 Inkreis, Umkreis, Schwerpunkt eines Dreiecks 6:03
!1!2 - 051 Rechtwinkliges Dreieck, Pythagoras 3:33
!1!2!3 - 052 Sinus, Cosinus, Tangens, Cotangens 6:00
- 053 Übliche Werte von Sinus und Freunden 6:23
- 053a Noch mehr Werte von Sinus und Freunden 3:47
- 054 Sinus, Cosinus, Tangens am Einheitskreis 5:29
!1!2!3!4 - 056 Additionstheoreme 6:45
- 057 Arcusfunktionen 4:10
!1 - 058 Sinussatz 5:01
- 059 Cosinussatz 6:35
- 061_062 Rechteck, Parallelogramm, Kreisumfang, Kreisfläche 8:07
- 063 Zylindervolumen 5:27
- 064 Volumen von Pyramiden und Kegeln 6:56
- 065 Kugelvolumen 5:39
- 066 Kugeloberfläche 7:10
- 067 Vektoren als Pfeile, Vektoraddition, Vektorsubtraktion, Vektor mal Skalar 7:44
!1 - 068 Vektorlänge, Nullvektor, Vektoren im Raum 4:15
- 069 Vektoren mit Zahlen schreiben 6:19
!1 - 070 Länge von Vektoren in Zahlen 3:34
- 071 Skalarprodukt in Zahlen 4:42
- 072 Skalarprodukt geometrisch 7:29
!1 - 073 weiter Skalarprodukt geometrisch 4:54
!1 - 074 Vektorprodukt in Zahlen 6:44
!1 - 075 Weitere Eigenschaften des Vektorprodukts 6:54
- 076 Vektorprodukt geometrisch 2:16
- 077 Mengen, Elemente, Teilmengen 6:02
!1!2!3 - 078 Vereinigung, Schnitt, Differenz, Komplement von Mengen 6:14
!1 - 079 Rechengesetze für Mengenoperationen; Venn-Diagramme 6:54
- 080 De-Morgan-Gesetze; disjunkte Mengen 4:10
!1!2!3 - 081 Typkorrektheit; Mengen von Mengen 4:04
- 082 Natürliche, ganze, rationale, reelle Zahlen und weitere Zahlenbereiche 7:06
!1 - 083 Mengenbildung durch Auswahl 4:23
- 084 Logische Operationen; Zahlenintervalle 6:08
!1 - 084a (095) Schnitt und Vereinigung von Intervallen 6:20
!1!2!3 - 085_086 Ungleichungen auflösen 11:09
- 087 Ableitung 7:15
- 088_089 Beispiel für Ableitung; Summe und Vielfaches ableiten; Produktregel 9:18
- 090 Kettenregel; Ableitung der Wurzelfunktion 5:14
- 091 Ableitung der Exponentialfunktion 4:07
- 092 Ableitung von Sinus, Cosinus, Logarithmus; Potenzregel; Quotientenregel 8:57
- 095a Lineare Gleichungssysteme zu Fuß lösen 6:14
- 096a Lösungsmengen linearer Gleichungssysteme 3:42
- 097 Quadratische Gleichung 10:55
- 098 Polynome, Grad, Nullstellen 5:33
- 099_100 Polynomdivision; Abspalten von Linearfaktoren 14:32
- 101 Faktorisierung von Polynomen 7:30
Mensch-Maschine-Interaktion Winter 2013/2014
14:08:57
- Mensch-Maschine-Interaktion; Anknüpfungspunkte mit der Elektrotechnik 20:24
- Themenideen zu Mensch-Maschine-Interaktion in diesem Semester 26:07
!1 - Elemente klassischer grafischer Oberflächen 21:23
- Einfache GOMS-Analyse grafischer Oberflächen 34:18
!1!2!3!4!5 - Erste Schritte mit Python und Qt 27:56
- Arbeit mit Qt Designer; Ereignisse; Zeitnahme; Dateien 23:57
!1 - GUI-Zeitmessungen an Programm mit Qt und Python 28:48
- Nachträge zu Python und Qt 5:00
- Regeln und Normen zur Gestaltung klassischer GUIs 24:36
- Das WWW. Geschichte, Funktionen, Rechtliches 31:50
- Aktuelle Technik des Web 9:08
- Web und Navigation 8:37
- Web; Kooperation und Dynamik 10:58
- Web; alte und neue Bedienelemente 15:43
- UIs prüfen mittels Cognitive Walkthrough 15:42
- Eye-Tracker für arme Leute, Teil 1 49:09
!1 - Eye-Tracker für arme Leute, Teil 2 37:25
!1!2!3 - Eye-Tracker für 100 Euro 3:02
- Typen von Usability-Untersuchungen 4:12
!1!2 - Multitouch; Historie und Standardgesten 14:46
- Multitouch mit Python und Qt; Pinch-Geste selbstgemacht 57:47
- Probleme von Touch-UIs 17:12
!1 - Nielsen und Landauer, A mathematical model of the finding of usability problems 14:05
- Greenberg und Buxton, Usability evaluation considered harmful (some of the time) 6:46
- Accelerometer und IMU; Gesten, Teil 1 52:15
- Accelerometer-Gesten, Teil 2 33:30
- Maschinenlernen, Gesten 1:03:12
- Accelerometer-Gesten mit einfachem Maschinenlernen 0:33
!1 - Sensoren und Aktoren für HCI 34:15
- HCI-Entwurfsprozess, Fallstricke 33:34
- HCI-Vorgehensmodelle 9:38
!1 - Gamification und Persuasive Computing 26:18
- Menschliche Wahrnehmung 25:04
!1!2 - Gesetze von Fitts und Hick 20:07
!1!2 - Diversity und Barrierefreiheit 10:34
- Menschliche Fehler, Aufmerksamkeit 31:06
!1
Mensch-Maschine-Interaktion Winter 2014/2015
12:24:47
- Zeit für Maus- und Tastatureingaben mit GOMS schätzen 13:32
!1!2 - Dialoge mit Qt Designer erstellen und in Python nutzen 45:06
- Python-Programm, das die Zeit zum Bedienen misst 33:07
- t-Test mit Tabellenkalkulation 42:52
!1!2 - HTML, CSS, JavaScript, PHP, AJAX in Aktion 50:11
!1!2 - EtherPad und draw.io als Beispiele für Web-Oberflächen 10:23
- Usability-Untersuchungen 3:53
- Eye-Tracker beobachtet Textlesen 10:47
- Cognitive Walkthrough für einen Bildkonvertierer 28:23
- Heuristiken für einen Bildkonvertierer 20:22
- Statistik des Fehlerfindens 15:02
- Informationsvisualisierung, Prinzipien 35:36
- Informationsanzeigen in Bus, Bahn und Auto 18:05
- einige Verfahren der Datenvisualisierung 29:35
!1!2!3!4 - Anleitungen als Teil der Mensch-Maschine-Schnittstelle 15:59
- Anleitung verständlicher formulieren 17:12
!1 - Multitouch-Ereignisse, Grundlagen der Programmierung 10:36
- Zehn-Finger-Malprogramm mit Multitouch in Python 1:00:37
- Pinch-Geste von Qt in Python nutzen 38:15
!1!2 - Mausgesten aufzeichnen und erkennen, Teil 1 55:01
!1 - Mausgesten aufzeichnen und erkennen, Teil 2 1:01:33
!1!2!3!4 - Activity-Tracker, Smart Watches und Datenbrillen 28:58
!1!2 - Methoden, um Kontext und Anforderungen für UI-Entwicklung zu erfassen 22:28
!1!2!3 - Spiralmodell und Methoden des Rapid Prototyping für UIs 19:41
!1 - JND, Gesetze von Weber-Fechner und Stevens, CIELAB 38:26
!1 - Gesetze von Fitts und Hick 13:02
- menschliche Fehler in Planung und Ausführung 6:05
Mensch-Maschine-Interaktion Winter 2015/2016
3:15:28
- Hypothesentest, p-Wert und weshalb man damit vorsichtig sein muss 32:08
!1!2!3!4 - Ideen hinter z-Test, t-Test, chi²-Test, ANOVA; Auswertung in Python 44:38
!1!2 - Zehn-Finger-Hockey mit Python und Qt 11:20
- Pebble-Smartwatch online programmieren 7:09
- Maschinenlernen anno 2015 38:08
- Maschinenlernen mit Python scikit-learn 14:02
- Gerade noch unterscheidbare Tonhöhenunterschiede mit Python finden 24:42
!1!2!3 - Persuasive Computing und Gamification vom Activity-Tracker bis hin zu Facebook 23:21
Mensch-Maschine-Interaktion Winter 2016/2017
6:04:24
- Mensch-Maschine-Interaktion, Überblick 31:00
- Python 3 auf die Schnelle 23:44
!1!2!3 - Mensch-Maschine-Interaktion, ein offener Online-Kurs 2:12
- Fitts‘ Gesetz, Messungen, Auswertung 17:41
!1 - Klassifikation menschlicher Fehler; Beispiele 7:04
- Handover; Computer übergibt Kontrolle an Mensch 7:01
- Erste Schritte mit PyQt5, Teil 1; Dialogbeschreibung laden 11:09
!1 - Erste Schritte mit PyQt5, Teil 2; Radio Button, Check Box 7:06
- Erste Schritte mit PyQt5, Teil 3; Dialog-Layout; modal, nichtmodal 8:37
- Erste Schritte mit PyQt5, Teil 4; Eingabefelder, Werte auslesen 10:27
!1 - Erste Schritte mit PyQt5, Teil 5; Menü, Tastaturkürzel, Tabulatorreihenfolge 12:20
- Erste Schritte mit PyQt5, Teil 6; Datei-Standarddialog 9:25
- Erste Schritte mit PyQt5, Teil 7; Zeichenfunktionen, Paint-Ereignis 17:10
- Kritik an Microsoft-Ribbons 3:07
!1 - Überblick HTML, CSS, JavaScript, PHP, Content-Management-Systeme 29:14
!1!2 - Multitouch-Ereignisse in PyQt 10:12
!1 - Perceived Affordances; Touch heißt noch nicht intuitiv 7:10
- Hostile Architecture; Soft- und Hardware mit eingebauten Verboten 4:01
- Sensoren im Smartphone; IMU 14:24
!1 - Intelligente Bedieninterfaces anno 2016 20:51
!1 - Neuronale Netze, SVM usw. mit scikit-learn 39:37
!1!2 - Persuasive Technology mit und ohne Computer 19:51
- Kritik an Persuasive Technology 4:48
- Cialdinis Prinzipien der Beeinflussung angewendet in Spam 7:27
- Warum so viele veröffentlichte Forschungsergebnisse falsch sind; Hypothesentest und Publication Bias 16:00
- p-Werte sind Zufallsgrößen; Signifikanzniveau 21:46
!1 - Abschluss des MOOC zur Mensch-Maschine-Interaktion 1:00
Projekt Solarprognose
0:44:29
- Kürzestfrist-Solarstromprognose 6:14
- mit C++ Daten aus Datei lesen 13:47
- OpenCV in Betrieb nehmen 24:28
Reisen durch die Raumzeit
14:54:01
- Lorentz-Transformationen 37:40
- Lorentz-Transformation im Detail 43:18
- relativistische Geschwindigkeitsaddition 17:40
!1 - Loedel-Minkowski-Diagramm; zweidimensionale Raumzeit 12:05
!1 - Längenkontraktion; Relativität der Gleichzeitigkeit 19:12
!1 - Zeitdilatation, Eigenzeit, Zwillingsparadoxa 25:43
- Viererimpuls, Masse und Energie 37:16
!1 - Überlichtgeschwindigkeit in der Speziellen Relativitätstheorie 17:41
!1 - Kovarianz, Kontravarianz, Tensoren 42:14
!1!2 - Ableitungen von Tensoren, metrischer Tensor 42:11
!1!2 - Viererstrom, Energie-Impuls-Tensor, Levi-Civita-Symbol 53:58
!1!2!3!4!5!6 - Äquivalenzprinzip, Geodäten, gekrümmte Raumzeit 54:27
!1!2!3!4!5!6!7!8 - Mannigfaltigkeiten, Tangentialräume, nochmals Geodäten 1:01:23
- kovariante Ableitung, Dichten, Divergenz 48:58
!1!2!3!4!5 - Riemannscher Krümmungstensor 23:26
!1!2!3!4 - Krümmungstensor = 0 30:11
!1!2!3!4!5!6 - kovariante Ableitungen vertauschen 17:58
- Symmetrien des Krümmungstensors 28:02
!1!2!3 - geodätische Abweichung, Deviationsgleichung 10:27
- Ricci-Tensor und Volumenänderung 22:07
!1 - Krümmungsskalar, Volumen eines geodätischen Balls 36:25
- Einsteinsche Feldgleichungen 19:58
!1 - Modell des Universums mit FLRW-Metrik, Friedmann-Gleichungen 55:18
!1!2!3 - Kosmologie der Friedmann-Gleichungen 38:38
!1!2 - Schwarzschild-Metrik und Schwarze Löcher 1:37:45
!1!2!3!4!5!6!7!8
Spezialthemen
7:52:41
- 1, 2, 4, 8, 16, 31; einen Kreis zerteilen 15:53
- Papier bis zum Mond falten 10:15
- Gödels Unvollständigkeitssätze 58:35
!1!2!3 - 1+2+3+4+… = 42 3:41
!1 - Die Maxwell-Gleichungen 51:45
- Inkreis eines Dreiecks 6:58
!1 - Error of the Forward Euler Method, LTE 13:04
!1 - Forward Euler Method, energy drift 26:35
!1!2 - Loviscach@Udacity: Making Math Matter — Differential Equations in Action 0:44
- Medical Test: Conditional Probability, Bayes‘ Theorem 9:50
- Hypothesis testing: one-/two-tailed z-test 15:49
!1!2 - Alle rationalen Zahlen aufzählen, Stern-Brocot, Calkin-Wilf 49:55
!1!2 - Zahlen mit möglichst einfachen Brüchen nähern, nach Stern-Brocot 26:23
- Fehler der Trapezregel für numerische Integration 20:07
- Ackermann-Funktion, primitiv rekursive Funktionen, Hyperoperationen 55:04
!1!2!3!4!5 - Impuls und Drehimpuls. Impulserhaltung 13:50
- Divergenz eines Vektorfelds 35:07
!1!2 - Rotation eines 2D-Vektorfelds 21:22
!1 - Rotation eines 3D-Vektorfelds, Satz von Stokes 37:44
!1
Talks and Demos
45:48:10
- Windenergie: Chancen & Probleme, Stand 2017 35:24
- Flipped Classroom: mit Videos die Präsenzzeit gewinnen 44:46
- Händewedeln in der Mathematik macht Spaß 38:50
- E Learning in den MINT-Fächern, ein kurzer Praxisbericht 19:01
- Jörn Loviscach: Zusammenfassung Themengruppe Innovationen in Lern- und Prüfungsszenarien 3:51
- Bildung steht nicht nur im Modulhandbuch — von den Gefahren einer naiven Digitalisierung 24:28
- #mevMOOC Der Abschluss und wie es weitergeht 1:48
- #mevMOOC Mathe endlich verstehen: Der Inhalt 2:18
- #mevMOOC – Mathe endlich verstehen – mit Jörn Loviscach 0:58
- Lernen mit Tests, Tests für das Lernen: E-Assessments ausschöpfen 42:23
!1!2 - Was Video kann. Und was nicht. Bewegte Bilder in der Hochschullehre 37:40
!1!2!3 - LoCoMoTion: techniques, methods and infrastructure for the low-cost production of MOOCs 18:51
!1 - E-Learning mit überschaubarem Aufwand 39:24
- Vom Frontal-MOOC zum Mitmachkurs 42:37
- Digitalisierung der Lehre: elektrifiziert oder elektrisierend? 36:27
- Mathematik schlicht und ergreifend 41:09
- Digitales Prüfen an der Hochschule 12:43
- Lernst Du noch oder verstehst Du schon? – 1. Tag der digitalen Lehre | Hochschule Fresenius 40:10
- Lehren ist unmöglich 57:17
- Videobasiertes Lernen 13:28
- Digitalisiertes Studium: Treiber, Effekte, Lektionen 26:32
!1!2 - Studieren wir bald nur noch virtuell? 46:50
- Why and how do explanation videos work? And do they? 9:38
- Vorlesungsfrei! Elektronische statt traditioneller Veranstaltungsformen 27:57
- Der Capira-Editor: Quizze über Videos legen 3:14
- Lernen mit Capira 1:38
- Teaching, Learning, Sharing 31:24
!1!2 - Lernen persönlich und elektronisch 41:30
!1 - MOOCs und Bildung: Neun gelernte Lektionen 43:38
- MOOCs in der akademischen Weiterbildung 23:03
- Erklärvideos in MOOCs und anderswo: didaktische und mediale Gestaltung 49:57
- Schätzen und Runden: Taschenrechner sind uncool 31:23
!1!2 - MOOCs: Wie verändern Online-Kurse die Hochschulen? (Expertentalk) 1:25:15
- Jörn Loviscach: Mit Videos lernen – ein Experimentierfeld 6:15
- MOOCs — Chance oder Risiko für die Hochschulweiterbildung? 39:50
- Digitale Beschulung ist noch keine Bildung 26:46
- MOOCs: Ist das Lehre oder kann das weg? 1:03:05
!1 - Der Flipped Classroom: Wie funktioniert der umgedrehte Unterricht? 56:30
- Friendly handmade explanation videos 12:55
- Digitale und analoge Illusionen der Bildung 57:08
- Die Welt mit xMOOCs retten? 21:22
- Massive Kurse und andere Mythen 56:18
!1 - Hochschullehre digital – Erfahrungen vom Seminar bis hin zum massiven Kurs – Jörn Loviscach 22:48
- Making Educational Videos Work in Mobile Settings 25:05
- Erklärvideos plus x statt Vorlesungen 38:49
- MOOCs, ein Überblick für Lehrende. Teil 1, die MOOC-Industrie 24:41
!1!2 - MOOCs, ein Überblick für Lehrende. Teil 2, Produktion und Durchführung 26:59
- MOOCs, ein Überblick für Lehrende. Teil 3, Didaktik 17:12
!1!2 - Auf der Suche nach der anschaulichsten Erklärung 36:50
- MOOCs und Weiterbildung 28:41
- Der elektrische Professor: E-Learning vs. Audimax?! 29:49
- Mathematik zum Mitmachen 50:30
!1 - Das Inverted Classroom Model 51:57
- 075: Studiertes, Gedrosseltes und Repariertes 14:17
- Die YouTubifizierung der Hochschule 28:02
- This –isn’t– shouldn’t be your parents‘ educational TV 34:52
- The Online Future of IT Education, sort of 41:45
- MOOC-Wettbewerb: Stimmen aus der Expertenjury 5:49
- Die Vorlesung ist tot, lang lebe die Vorlesung!? 56:45
!1 - MOOCs: 50+ years of open education for massive audiences 32:59
!1!2 - Der Inverted Classroom: ein Vehikel für offene Lehr- und Lernmaterialien? 48:12
- re:publica 2013 – Sebastian Wernicke, Jörn Loviscach: Online universities – food for thought or an i 27:48
- Erfahrungen mit der Lehre per Video und xMOOC 43:00
- Der elektrische Professor 47:13
- Videos in der Hochschullehre, konkrete Nutzung 23:52
!1 - Bessere MOOCs für bessere Lehre 44:46
- MOOCs and other faster horses 48:12
- Millions of Lessons Learned on Electronic Napkins 36:32
!1 - Visual Explanations with Lean Technology: Mathematics and Computer Science on YouTube 23:40
!1 - The environmental cost of Bitcoin 24:20
!1 - Jörn Loviscach: E-Learning – Chancen und Grenzen 7:35
- Vorlesungsaufzeichnungen auf YouTube. Herausforderungen, Werkzeuge, Erfahrungen 41:41
!1!2!3!4!5 - Typeface Styling with Ramp Responses 1:23
- Unfassbar anfassbar, denkbar lenkbar: Wohin nun? 40:06
- Wo kommen eigentlich die Handys her? 16:44
- Educating Artist-Inventors 26:31
- Transcending the Status Quo (in HCI and Digital Media) 24:09
- YouTube: Formeln und anonyme Kommentare 3:51
!1 - Virtual Board: Demo 2:51
- Poor Man’s Thermographic Camera 2 6:50
- Soundtorch 2.0 2:13
- A Nimble Editor for Videocasts 2:32
!1 - Ray-traced GUIs for audio effect plug-ins 3:11
!1 - A graphics tablet as transparent blackboard 3:37
!1 - Wii-mote Foley Demo @ TEI 2011 Conference. 0:26
- 01 Semantische Audioanalyse 10:31
!1 - 02 Semantische Audioanalyse 5:46
!1 - 03 Semantische Audioanalyse 5:44
- 04 Semantische Audioanalyse 8:19
!1!2 - 05 Semantische Audioanalyse 7:18
!1!2 - 06 Semantische Audioanalyse 10:01
- 07 Semantische Audioanalyse 2:52
- 08 Semantische Audioanalyse 8:36
- 09 Semantische Audioanalyse 4:34
!1 - 10 Semantische Audioanalyse 10:06
- 11 Semantische Audioanalyse 7:44
- 12 Semantische Audioanalyse 5:00
- 13 Semantische Audioanalyse 9:31
- 14 Semantische Audioanalyse 5:15
- 15 Semantische Audioanalyse 6:24
!1!2 - 16 Semantische Audioanalyse 2:57
- Lighting Control through Laser Pointer Gestures 7:23
- Google und die Waschmaschinen, Teil 1 von 3 8:41
!1 - Google und die Waschmaschinen, Teil 2 von 3 6:44
- Google und die Waschmaschinen, Teil 3 von 3 6:36
!1 - Pus in Motion 0:50
- Listening Wind: Music Visualization 4:32
- Procedural Plants for Music 1:21
!1 - FlexiKnobs: Multipoint Interaction with Audio Software 1:57
- Atomic Sounds: Generic Sound Effects to Aid in Audio Retrieval 1:53
- A Loudspeaker as Drumhead 4:25
- Projecting Finger Placement onto the Fretboard 2:13
- Trailer: YouTube for the Poor & Lazy Professor 0:55
- Graphical Control of a Parametric Audio Equalizer 6:27
- Enhanced Faders 3:40
- Automatic Adjustment of Off-the-Shelf Reverberation Effects 3:34
- SonoSketch 3:14
- Soundtorch 2:01
- Poor Man’s Thermographic Camera: two Approaches 1:58
!1!2!3 - A Random Cursor Matrix to Hide Graphical Password Input 0:50
- Aurally and Visually Enhanced Audio Search 37:10
- NoISE Final Presentation Part 1/4 9:54
- NoISE Final Presentation Part 2/4 9:44
- NoISE Final Presentation Part 3/4 9:52
- NoISE Final Presentation Part 4/4 7:20
- HCI: Studierende forschen, Teil 1 von 6 9:17
- HCI: Studierende forschen, Teil 2 von 6 9:16
- HCI: Studierende forschen, Teil 3 von 6 9:20
- HCI: Studierende forschen, Teil 4 von 6 9:17
- HCI: Studierende forschen, Teil 5 von 6 9:16
- Complex Water Effects on the GPU 1:00
- HCI: Studierende forschen, Teil 6 von 6 5:05
- Two-Finger Input with a Standard Touch Panel 1:58
- Efficient Magnification of Bi-Level Textures 0:51
- File Icons that Show the Content of Audio Files 2:20
- Stylized Haloed Outlines on the GPU, 1 of 2 0:08
- Stylized Haloed Outlines on the GPU, 2 of 2 0:08
- Walking with Pens: 3D Motion Input 0:56
- Grunge Style for 3D Objects, Fully Automated 0:40
!1!2!3!4!5
Udacity CS222 Highlights
0:40:58
- Leonard Susskind – Physics Is Differential Equations – Differential Equations in Action 2:36
- Derivative Overview – Differential Equations in Action 4:18
- Shell Theorem – Differential Equations in Action 3:59
- 圆形轨道 2:44
- Heun 方法 2:54
- 偶对求解程序 1:11
- The SIR Model – Differential Equations in Action 2:01
- Vaccination – Differential Equations in Action 0:49
- Dahlquist’s Test Equation – Differential Equations in Action 1:32
- Logistic Growth – Differential Equations in Action 1:35
- Fish Modeling – Differential Equations in Action 0:45
- Derivative of Exponential Function – Differential Equations in Action 1:57
- Wheel Slip – Differential Equations in Action 2:06
- Central Difference Derivation – Differential Equations in Action 4:01
- Heat Equation – Differential Equations in Action 2:23
- Partial Derivatives – Differential Equations in Action 1:02
- Heat Equation in 2D – Differential Equations in Action 0:48
- Finite Element Method – Differential Equations in Action 2:45
- The Lorenz System – Differential Equations in Action 1:32
Wind- und Wasserkraft, Winter 2014/2015
19:41:59
- Wind- und Wasserkraft, Themenüberblick 12:41
- Unterschiede Wind- und Wasserkraft 5:39
- Weltbevölkerung mittels Windenergie versorgen 18:22
- Aufstellungsdichte der Windturbinen für Vollversorgung 4:48
- Deutschland mittels Wasserkraft versorgen 19:00
- grundlegende Formeln Wind- und Wasserkraft 4:26
- Windentstehung; Überblick, Grundbegriffe 5:33
- Windentstehung; Coriolis-Kraft; Wolkenbildung und Niederschlag 17:39
!1 - Passat-Winde, Hadley-Zellen 22:38
!1 - Winde zwischen Land und See 3:39
- Hochs und Tiefs; geostrophischer Wind 9:40
- Drehrichtung eines Tornados 3:33
- Windrichtung aus Isobaren schließen 7:27
!1 - Kraft auf Luft durch Druckunterschied 11:03
- Warum Windstatistik; Windenergieberechnung mit Tabellenkalkulation 24:20
!1 - Weibull- und Rayleigh-Verteilungen für Windgeschwindigkeit 19:41
!1!2 - Windprofil logarithmisch und als Potenzgesetz 15:19
!1!2 - Rauigkeitslänge aus Windgeschwindigkeiten in zwei Höhen 12:21
- Grundideen Fluiddynamik; Euler-Gleichungen 39:51
!1 - Auftrieb; warum ein Flugzeug fliegt 16:53
!1!2 - Luftwiderstandand und Auftrieb; Beiwerte 18:10
- Endgeschwindigkeit mit Fallschirm 3:30
!1 - Flugzeug vs. Senkrechtstarter-Bus 3:24
- gegen den Wind segeln 5:49
- Drehmoment eines Schalen-Anemometers 10:05
- Gleitzahl und Gleitflug 9:23
- Anstellwinkel, Strömungsabriss 5:34
!1!2!3!4 - maximaler Leistungsbeiwert einer Windturbine; Betzsches Gesetz 34:31
!1!2 - Durchmesser der Windturbine ändern, wenn Generator stärker 6:09
- Windgeschwindigkeit aus Leistung der Windturbine 5:46
- Schubkraft auf den letzten Meter eines Rotorblatts 10:53
- kurze Geschichte der Windenergienutzung 10:14
!1!2 - Schnelllaufzahl einer Windturbine 15:55
!1 - optimale Form der Rotorblätter einer Windturbine 26:52
- Kräfte auf ein Rotorblatt einer Windturbine 39:28
!1 - mechanische Komponenten einer Windkraftanlage 8:20
- Schwingungen einer Windkraftanlage; Campbell-Diagramm 18:34
- Übersetzung des Getriebes einer Windkraftanlage 8:01
!1!2 - Wärmeabfuhr aus Getriebe einer Windkraftanlage 11:25
!1 - nötige Getriebeübersetzung für Windkraftanlage 3:46
!1 - Zeigerdiagramme; komplexe Wechselstromrechnung 11:32
- Kondensator und Induktivität als komplexe Widerstände; Zeigerdiagramm 10:55
- Verschiebungsfaktor für Widerstand und Kondensator parallel 7:07
- Warum Drehstrom; Summe; Summe der Quadrate 11:02
- Synchrongenerator, über- und untererregt, Blind- und Wirkleistung 31:34
!1 - Synchrongenerator mit zwölf Polen, elektrisch oder permanent erregt 13:32
!1 - Synchrongenerator mit Umrichter 6:44
!1!2!3 - Asynchrongenerator, Schlupf 8:07
- Prinzip des Asynchrongenerators; Käfigläufer 23:59
!1 - Ersatzschaltbild des Asynchrongenerators 21:26
- weitere Asynchrongeneratoren, doppelgespeister Asynchrongenerator 7:33
- Generatorkonzepte für Windenergie 7:24
- WKA, Mittelspannung, Transformator 14:27
- WKA am Mittelspannungsnetz; Technische Richtlinie 35:21
- Spannungsanhebung durch Einspeisung 35:17
!1 - Spannungsanhebung durch Einspeisung; Beispielrechnung 27:35
- Wirkungen einer Windkraftanlage auf die Umwelt und umgekehrt 12:32
- Schallimmissionen, dB(A), Abfall mit Entfernung 31:28
!1 - Entfernung bestimmen für 20 dB weniger Lärm 11:09
- Entfernung ändern, damit um 1 dB lauter 9:32
- Schattenwurf in Abhängigkeit von Jahres- und Tageszeit 33:11
!1!2!3!4!5!6 - Größe der Sonnenscheibe im Vergleich zu Fingernagel 5:09
- längster und kürzester Schatten mittags 12:57
- Schattenrichtung am 21. Juni morgens berechnen 33:34
- Schattenrichtung am Äquator am 21.12. bei Sonnenuntergang 3:16
- Habitat- und Artenschutz 9:15
!1!2!3 - Windkraftanlage regeln; Stall und Pitch 31:23
!1!2!3!4 - Jahresenergie aus einfacher Windstatistik 5:39
- Energieertrag WKA mit gleichem Rotor, aber verschiedener Nennwindgeschwindigkeit 7:38
- Windparks, offshore 17:47
- Windkraftanlage hinter Horizont verstecken 5:27
- Windpark-Layout 6:07
!1 - Wasserkraft, Geschichte, Generatoren 4:45
- Satz von Bernoulli; Druck und Geschwindigkeit 15:44
- Beispiele für Satz von Bernoulli; horizontales Rohr 10:51
- Energie in fließendem Wasser 2:47
- Energie in ruhender Wassersäule 4:14
- Leistung in einem Wasserstrahl aus 1500 m Höhe 7:27
- Drei Arten Wasserkraft; Physik 14:28
- spezifische Drehzahl n_q einer Wasserturbine; Typen 19:27
- Wasserturbinen nach Pelton, Francis, Kaplan 36:10
!1!2 - Drehzahl Pelton-Turbine aus Fallhöhe 4:48
- ungewöhnliche Arten von Windkraftanlagen 15:30
- ungewöhnliche Arten von Wasserkraftanlagen 5:47
!1
Wind- und Wasserkraft, Winter 2015/2016
15:18:58
- Jahresenergieertrag eines vereinfachten Gezeitenkraftwerks 15:13
- Jahresenergieertrag einer Windkraftanlage mittels Windstatistik 14:44
- Windentstehung, Monsun, Passat, Hoch und Tief 10:13
!1 - Corioliskraft, rotierendes Koordinatensystem 24:50
- Corioliskraft auf Wasser im Abfluss 9:08
- Geschwindigkeit des geostrophischen Winds 12:54
- Wind auf Inertialkreisen 8:48
- Gradientenwind; Entstehung von geostrophischem Wind; subgeostrophischer Wind 15:42
- Rayleigh-Verteilung als einfaches Modell der Windstatistik 21:58
!1 - Windprofil; Nabenhöhe und Leistung einer WKA 10:22
!1 - Amsel und Airbus A380, Skalierung von Größe und Geschwindigkeit 22:24
!1 - Strömungsabriss beim langsamen Flug in horizontaler Richtung 3:24
- Starten und Landen mit oder gegen Wind 1:32
- Auslenkung einer Kugel durch Wind 8:22
- Fallgeschwindigkeit eines stromlinienförmigen Objekts 4:30
- Größe von Windkraftanlagen skalieren 7:18
- Skalierung von Ertrag und Kosten von Windkraftanlagen, Grenzen des Square-Cube Law 22:22
- Betzscher Leistungsbeiwert auf die Schnelle 11:19
- Schnelllaufzahl und Skalenverhältnisse 9:16
- Winddreieck, Blattprofil, Auftrieb, Strömungswiderstand 10:22
- Mechanische Komponenten einer WKA; Blattverstellung, Pitchwinkel 11:09
- Beispielrechnungen Generatorfrequenz und Getriebeübersetzung 7:59
- Masse des Betonturms für eine Windkraftanlage; Modell für Statik 31:12
- Einfacher Synchrongenerator; Induktion, Lenzsche Regel, Lorentz-Kraft 18:00
- Beispielrechnung Verschiebungsfaktor 7:23
!1 - Generatorkonzepte für Windkraftanlagen, kurzgefasst 4:27
- Wiederholung Zeigerdiagramm, Blindwiderstand, Impedanz 29:05
- Spannungsanhebung bei Einspeisung; Wirkung der Blindleistung 55:33
- Schalldruckpegel um 12 dB senken; Änderung der Schallleistung 9:40
- Stelle mit gleichem Schallpegel zwischen zwei Schallquellen 18:52
- Schalldruckpegel in Wasser auf Luft umrechnen 18:10
- Schattenlänge am 21. März mittags; Schattenverlauf über das Jahr 12:38
- Entfernung, damit WKA-Rotor so groß wie Sonnenscheibe 4:17
- Regelung einer Windkraftanlage anhand der Windgeschwindigkeit 27:13
!1!2!3!4!5 - Regelung einer Windkraftanlage anhand der Drehzahl 22:13
- Ertragsprognose für eine Windkraftanlage 47:14
- Windturbine hinter Horizont, trotz erhöhter Betrachtungsposition 8:44
- Kabel; Herleitung der Leitungsgleichungen mit Zeigern 24:54
!1 - Physik der Wasserkraft; Kontinuität, Leistung, Bernoulli 23:25
- Staudruck, dynamischer Druck; Prandtl-Rohr, Saugschlauch 18:53
!1!2 - Kavitation 20:50
!1 - Umweltaspekte der Wasserkraft 9:32
- Saugschlauch, Bernoulli, Kavitation 12:10
- Pumpspeicherkraftwerke am Beispiel Goldisthal 11:49
- Spekulative Formen von Pumpspeicherkraftwerken 51:59
- Beispiel für Auftrieb und Strömungswiderstand am Darrieus-Rotor 4:41
- Erneuerbare-Energien-Gesetz EEG, Stand Januar 2016 32:06
!1!2 - Förderung von Windkraft nach § 49 EEG 2014; Referenzertrag 35:43
!1!2!3!4 - Messung an Windturbine vs. Betz 3:51
- Segelflugzeug und Wasserballast 11:42
!1 - Drehzahl einer durchgehenden Pelton-Turbine 9:37
!1 - Komplexe Last am Generator 14:28
!1 - Geschwindigkeitsmessung über Druckdifferenz an Verengung 7:12
- Verlauf von Druck und Geschwindigkeit bei Pelton- und Francis-Turbine 22:56
- Schubkraft auf Windkraftanlage mit Betz schätzen 12:29
!1 - kritische Geschwindigkeit für Kavitation bei Turbine unterhalb Unterwasserspiegel 6:12
- Zentrifugalkraft auf 1 m³ Luft 5:59
Wind- und Wasserkraft, Winter 2016/2017
10:55:43
- Windenergie und Umwelt, ein offener Online-Kurs 1:44
- Energiebilanz von Windenergie, Einführung 3:58
- Der Erntefaktor als dehnbare Kennzahl 10:58
- Energetische Amortisationszeit 8:34
!1 - Materialien und CO2-Bilanz eines Windparks 34:59
- Neodym in Windturbinen 7:36
- Linien gleichen Schalldruckpegels um WKA 6:03
- Überlagerung des Schalldruckpegels zweier WKA 11:49
- Rotor einer WKA skalieren; Masse, Leistung, Schnelllaufzahl 2:51
- Schallintensität einer und mehrerer Windturbinen; Kohärenz 5:22
- Warum es nachts und in Windrichtung lauter ist 6:09
!1 - Verringerung der Schallemissionen von WKA 5:54
!1 - Schalleistungspegel und Schalldruckpegel, Teil 1 13:15
- Schalleistungspegel und Schalldruckpegel, Teil 2 13:46
- ebene Schallwelle; Schalldruck, Schallintensität, Schallschnelle 34:25
- Infraschall und Windenergie 3:30
- Licht und Schatten an einer Windkraftanlage 3:54
- Schattenwurf einer WKA; Sonnenscheibe 6:42
- kürzester Abstand zwischen Turm und Rotorschatten einer WKA 3:29
- Simulation des visuellen Eindrucks von Windkraftanlagen 17:35
- Sichtbarkeit von Windkraftanlagen 9:50
- Einige Faktoren der visuellen Wirkung von WKA 5:56
- Einige rechtliche Vorgaben zu WKA und Abständen 9:37
- Windenergie und Habitat- und Artenschutz 6:28
- Windturbinen und Vögel 18:47
!1 - Windturbinen und Fledermäuse 7:42
- Windturbinen und Schweinswale 9:59
- Brände, Unfälle usw. an Windturbinen 1:19
- Brände von Windkraftanlagen 13:37
!1!2 - Abreißen von Rotorblättern, Havarie von WKA 22:08
!1!2 - Unfälle durch Windenergie 9:37
!1!2!3 - Freisetzung von Schadstoffen durch WKA 3:03
- Netzintegration von Windenergie 5:46
- Windenergie und Regelleistung, Teil 1; Netzfrequenz und Regelungstypen 12:08
- Windenergie und Regelleistung, Teil 2; Regelleistung aus Wind 5:22
- Windenergie und Regelleistung, Teil 3; Trägheit und Instabilität 9:22
- Windenergie und Regelleistung, Teil 4; Momentanreserve aus Windturbinen 8:47
!1 - Speicherung von Windenergie 10:19
- Transport von Windstrom 5:12
!1 - Windenergie und Umwelt, Abschluss 1:37
- Windenergietechnik, ein offener Online-Kurs #windtechMOOC 1:44
- #windtechMOOC Ablauf und Organisation 2:06
- Gradientenkraft auf Luft 12:20
- Corioliskraft, geostrophischer Wind 15:27
!1!2 - schnell zu Formeln für Corioliskraft und Zentrifugalkraft 8:33
!1 - Windstatistik, Rayleigh-Verteilung 22:24
- Änderungen im Windprofil durch EEG 2017 12:50
- Sieben Begriffe aus der Aerodynamik 5:06
- Windenergie aus Strömungswiderstand; Leistungsbeiwert 19:37
- Leistungsbeiwert mit bodennah gemessener Windgeschwindigkeit 7:20
- Jahreserträge mit viel zu einfacher Windstatistik vergleichen 4:25
!1!2 - Elektromagnetismus ohne Formeln 16:53
- Nord- und Südpol an einer Spule 2:50
- Kräfte auf einen Magneten in einem Magnetfeld 17:27
- Kraft auf bewegte Ladung oder Induktion durch veränderliches Magnetfeld 7:04
- Wirk-, Schein- und Blindleistung 24:55
- Verschiebungsfaktor für R parallel C, Leistung gegeben 6:31
- Spule in Reihe mit Kondensator und Widerstand parallel; komplexe Wechselstromrechnung 11:47
- Regelung einer WKA; Leistung, Drehzahl, Pitchwinkel 6:55
- Gebäudeintegrierte Windturbinen 6:06
- Aufwindkraftwerk 4:05
- EEG 2017, Änderungen im Erneuerbare-Energien-Gesetz 16:50
- Windenergietechnik-MOOC, Abschluss und Ausblick 2:16
- Druck in Leitung; Bernoulli angewendet 3:40
- Druck vor Saugschlauch eines Wasserkraftwerks 10:40
- Satz von Bernoulli in einer Rohrkonstruktion 10:36
- Rechenbeispiel Wellenenergie; Wasserverdrängung und Auftrieb 7:47
- Wellenenergie aus pneumatischer Kammer; Wells-Turbine 8:20