|
Bild: self Georg-Johann Lay, Public domain, via Wikimedia Commons
|
|
Das Sierpinski-Dreieck ist ein 1915 von Wacław Sierpiński beschriebenes Fraktal[1] – mitunter auch Sierpinski-Fläche oder -Dichtung genannt, welches eine selbstähnliche Teilmenge eines meist gleichseitigen Dreiecks ist. Teilt man das Dreieck in vier zueinander kongruente und zum Ausgangsdreieck ähnliche Dreiecke, deren Eckpunkte die Seitenmittelpunkte des Ausgangsdreiecks sind, dann sind die Teilmengen des Fraktals in den drei äußeren Dreiecken skalierte Kopien des gesamten Fraktals, während das mittlere Teildreieck nicht zum Fraktal gehört. Diese Aufteilung des Fraktals in skalierte Kopien kann in den äußeren Teildreiecken rekursiv fortgesetzt werden. Die fraktale Dimension des Sierpinski-Dreiecks beträgt
- D=log23≈1,58496…
Konstruktion
Algorithmus
Zur Darstellung des Sierpinski-Dreiecks wird als Ausgangsdreieck meist ein gleichseitiges Dreieck gewählt. Das ist nicht zwingend; aus jedem Dreieck kann ein Sierpinski-Dreieck erzeugt werden.

Der klassische Algorithmus, der zur grafischen Demonstration des Fraktalbegriffs verwendet wird, ist folgender:
- Zeichne ein Dreieck („Initiator“)
- Verbinde die Mittelpunkte der Seiten („Generator“). Dadurch wird das ursprüngliche Dreieck in 4 deckungsgleiche Teildreiecke zerlegt.
- Entferne das mittlere der 4 Teildreiecke. Die anderen 3 Teildreiecke bleiben übrig.
- Wende Schritte 2 und 3 auf die drei übriggebliebenen Teildreiecke an usw.

Dieser Algorithmus verdeutlicht den Zusammenhang. Bei jedem Iterationsschritt entstehen an den Ecken 3 zum Initiator ähnliche Dreiecke mit halber Seitenlänge und 1/4 des Flächeninhalts, die gefärbt werden. Das 4. innere kleine Dreieck, welches dabei entsteht, kann man sich als aus der Dreiecksfläche des vorhergehenden Schritts herausgeschnitten vorstellen.
Das eigentliche Sierpinski-Dreieck im streng mathematischen Sinn ist diejenige Punktmenge, die als „Grenzobjekt“ nach unendlich vielen Iterationsschritten übrigbleibt. Anschaulich gesprochen besteht das Sierpinski-Dreieck somit aus unendlich vielen Eckpunkten. Zur Darstellung, die meist mit rekursiven Computerprogrammen realisiert und nach Bedarf auf einem Bildschirm angezeigt oder ausgedruckt wird, reicht meist schon eine Iterationstiefe oder Rekursionstiefe von höchstens 10. Bedingt durch die Bildauflösung des darstellenden Mediums (Monitor, Drucker etc.) und des menschlichen Auges sind diese Gebilde vom Grenzobjekt nicht mehr zu unterscheiden. In klassischer planimetrischer Flächenmessung geht der Flächeninhalt mit zunehmender Iterationstiefe gegen 0.
Die folgende Tabelle zeigt die Anzahlen der verschiedenen Teildreiecke des Sierpinski-Dreiecks nach k Iterationsschritten für k ≤ 4 :
| Anzahl der Teildreiecke | ||||
|---|---|---|---|---|
| Iterationsschritt | übriggeblieben | neu gelöscht | insgesamt gelöscht | insgesamt |
| k | 3k | 3k − 1 | (3k − 1) / 2 | (3k + 1 − 1) / 2 |
| 0 | 1 | 0 | 0 | 1 |
| 1 | 3 | 1 | 1 | 4 |
| 2 | 9 | 3 | 4 | 13 |
| 3 | 27 | 9 | 13 | 40 |
| 4 | 81 | 27 | 40 | 121 |
Lindenmayer-System
Das Sierpinski-Dreieck lässt sich durch ein Lindenmayer-System mit folgenden Eigenschaften beschreiben:
- Winkel: 120°
- Startstring: A + A + B
- Ableitungsregeln:
- A↦AA
- B↦B+A−B−A+B
Darstellung in Wolframs eindimensionalem Universum
In Stephen Wolframs eindimensionalen zellulären Automaten erzeugt eine einzelne lebende Zelle in Regel 90 ein Sierpinski-Dreieck.
Mathematische Zusammenhänge

Als klassisches Fraktal ist das Sierpinski-Dreieck ein Musterbeispiel für exakte Selbstähnlichkeit: Die in jedem Schritt erzeugten äußeren Teildreiecke enthalten verkleinerte exakte Kopien des gesamten Fraktals. Eine passende Skalierung eines beliebigen dreieckigen Teils des Fraktals erscheint wie das Gesamtobjekt selbst. Es ist somit skaleninvariant.
Nach k Iterationsschritten bleiben 3 k Teildreicke gleicher Seitenlänge übrig und es werden 3 k − 1 2 Dreiecke verschiedener Seitenlänge entfernt.
Flächeninhalt
Wenn das ursprüngliche Dreieck (Ausgangsdreieck) gleichseitig ist und die Seitenlänge a hat, beträgt sein Flächeninhalt A 0 = 3 4 ⋅ a 2 .
Dann sind offensichtlich auch alle Teildreiecke und alle gelöschten Dreiecke gleichseitig. Beim ersten Iterationsschritt wird ein Dreieck mit halber Seitenlänge, also dem Flächeninhalt 3 16 ⋅ a 2 entfernt. Mit jedem Schritt verdreifacht sich die Anzahl der Dreiecke und die Seitenlänge halbiert sich, sodass beim Iterationsschritt k genau 3 k − 1 Dreiecke mit der Seitenlänge a 2 k entfernt werden. Der Flächeninhalt der gelöschten Dreiecke beim Iterationsschritt k ist also gleich 3 k − 1 2 2 ⋅ k ⋅ 3 4 ⋅ a 2 = ( 3 4 ) k ⋅ 3 12 ⋅ a 2 . Der gesamte Flächeninhalt der gelöschten Dreiecke nach dem Iterationsschritt k ist also gleich ∑ i = 1 k ( 3 4 ) i ⋅ 3 12 ⋅ a 2 = ( 1 − ( 3 4 ) k + 1 1 − 3 4 − 1 ) ⋅ 3 12 ⋅ a 2 = ( 1 − ( 3 4 ) k ) ⋅ 3 4 ⋅ a 2 und der Flächeninhalt der übriggebliebenen Teildreicke ist gleich A k = ( 3 4 ) k ⋅ 3 4 ⋅ a 2 . Dabei wurde eine so genannte geometrische Reihe mit dem konstanten Skalierungsfaktor 3 12 ⋅ a 2 berechnet.
Das lässt sich auch einfacher erkennen, denn mit jedem Iterationsschritt verringert sich der gesamte Flächeninhalt, der am Anfang A 0 = 3 4 ⋅ a 2 beträgt, um 1 4 , oder anders ausgedrückt, er multipliziert sich mit dem Faktor 3 4 . Nach k Schritten ergibt sich logischerweise der Flächeninhalt A k = ( 3 4 ) k ⋅ 3 4 ⋅ a 2 , der sich auf 3 k Teildreiecke mit der Seitenlänge a 2 k aufteilt.
Der Flächeninhalt der übriggebliebenen Teildreiecke geht gegen 0, wenn die Anzahl k der Schritte gegen unendlich geht. Formal lässt sich das mit lim k → ∞ A k = lim k → ∞ ( 3 4 ) k ⋅ 3 4 ⋅ a 2 = 0 ausdrücken. Entscheidend ist dabei, dass die Seitenlänge a konstant bleibt. Bei einigen anderen Fraktalen, zum Beispiel der Koch-Kurve, der Mandelbrot-Menge und vielen Julia-Mengen, nähert sich der Flächeninhalt stattdessen einem konstanten Wert größer als 0, konvergiert also auch.
Fraktale Dimension
Von den zugrundeliegenden mathematischen Gesetzmäßigkeiten her ist das Sierpinski-Dreieck eng verwandt mit der Cantor-Menge. Seine fraktale Dimension ist der Kehrwert derselben, nämlich log ( 3 ) log ( 2 ) ≈ 1,585 . Dies resultiert daraus, dass sich die Anzahl der Teildreiecke mit jedem Schritt verdreifacht, also beim Schritt k genau 3 k neue Teildreiecke mit der Seitenlänge a 2 k erzeugt werden. Das Fraktal entsteht als Grenzobjekt, wenn k gegen unendlich geht, genauer, indem der Durchschnitt aller Zwischenschritte der Konstruktion gebildet wird, und es kann daher als „geometrisches Analogon“ zu einem Grenzwert aufgefasst werden. Aus der Bildungsvorschrift lässt sich auch berechnen, welche Punkte der ursprünglichen Fläche zum Grenzobjekt gehören.
Zusammenhang mit regelmäßigen Parkettierungen
Das regelmäßige Sierpinski-Dreieck steht im Zusammenhang mit dem regelmäßigen Dreiecksgitter, das die euklidische Ebene vollständig mit kongruenten gleichseitigen Dreiecken ausfüllt (siehe Abbildung). Dieses regelmäßigen Dreiecksgitter ist spiegelsymmetrisch, punktsymmetrisch, drehsymmetrisch und translationssymmetrisch und eine sogenannte platonische Parkettierung (englisch: uniform tiling).
Das regelmäßige Dreiecksgitter ist eine feinere Zerlegung des regelmäßigen Sierpinski-Dreiecks nach dem Iterationsschritt k . Dabei werden die gelöschten Dreiecke des Iterationschritts i , deren Seitenlänge um den Faktor 2 k − i größer als die Seitenlänge der übriggebliebenen Dreiecke ist, jeweils in ( 2 k − i ) 2 = 4 k − i kongruente gleichseitige Dreiecke mit dieser Seitenlänge zerlegt. Das äußere Gebiet, das theoretisch ins Unendliche der zweidimensionalen Ebene geht, wird ebenfalls in solche Dreiecke zerlegt. Das regelmäßige Sierpinski-Dreieck nach dem Iterationsschritt k überdeckt ziemlich offensichtlich 4 k Dreiecke des regelmäßigen Dreiecksgitters.
Die kongruenten Dreiecke müssen nicht gleichseitig sein. Mithilfe einer affinen Abbildung kann das Sierpinski-Dreieck zusammen mit dem Dreiecksgitter auf beliebige Dreiecke verallgemeinert werden.
-
Allgemeines Dreiecksgitter
Topologie
In der Topologie betrachtet man das Sierpinski-Dreieck als Unterraum des mit der euklidischen Metrik versehenen R 2 . Es stellt ein im R 2 nirgends dichtes, lokal zusammenhängendes, metrisches Kontinuum dar und gilt – zusammen mit dem Sierpinski-Teppich – nicht zuletzt deswegen als besonders bemerkenswerter topologischer Raum.[2]
Darstellung mittels Hutchinson-Operator
Ein Sierpinski-Dreieck lässt sich auch als Attraktor eines dynamischen Rückkopplungsprozesses, eines deterministisch iterierten Funktionensystems mit geeigneten Parametern aus nahezu jeder beliebigen geometrischen Figur darstellen. Dabei werden wiederholt Mehrfach-Transformationen des Ausgangsobjektes vorgenommen, diese Bilder mit einer Abbildungsvorschrift, dem Hutchinson-Operator, entsprechend angeordnet und diese Prozedur erneut auf das entstandene Gesamtbild angewandt usw. Mit zunehmender Iterationstiefe streben die entstehenden Bilder, falls geeignete Parameter gewählt wurden, einem Sierpinski-Dreieck zu, das in diesem Falle der Attraktor des Funktionensystems ist.
Das Sierpinski-Dreieck ist in diesem Sinne charakterisiert als diejenige kompakte Teilmenge der Ebene, die identisch ist mit der Vereinigung ihrer drei Bilder unter den drei Ähnlichkeitsabbildungen, die das gesamte Dreieck jeweils auf die drei halb so großen Teildreiecke abbilden.
 |
 |
 |
 |
 |
 |
 |
 |
|
| Stufe | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
Sierpinski-Pfeilspitzen-Kurve

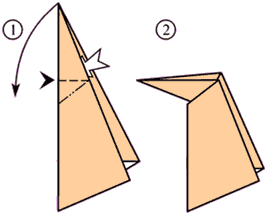
Die Sierpinski-Pfeilspitzen-Kurve (siehe Abbildung) ist eine raumfüllende Kurve, die das Sierpinski-Dreieck in der zweidimensionalen euklidischen Ebene approximiert. Die Sierpinski-Kurve oder auch die Hilbert-Kurve oder die Peano-Kurve haben andere fraktale Eigenschaften und keinen direkten Zusammenhang zum Sierpinski-Dreieck.
Die fraktale Selbstähnlichkeit der Sierpinski-Pfeilspitzen-Kurve ist komplizierter, weil dort andere Drehungen, Spiegelungen und lokale Ungenauigkeiten eine Rolle spielen.
Sierpinski-Tetraeder

Eine Darstellung des Sierpinski-Dreiecks ist, analog zum Menger-Schwamm, auch dreidimensional möglich: Die Startfigur ist ein Tetraeder. Aus dessen Mitte wird in jedem Iterationsschritt ein Oktaeder mit halber Kantenlänge herausgeschnitten. Übrig bleiben vier Tetraeder, aus denen wieder je ein Oktaeder herausgeschnitten wird usw.[3]
Nach dem Iterationsschritt k sind offensichtlich 4 k Teil-Tetraeder mit derselben Seitenlänge entstanden. Die Anzahl der herausgeschnittenen Oktaeder mit verschiedener Seitenlänge beträgt 4 k − 1 3 .
Die Dimension für dieses Gebilde ist D = log ( 4 ) log ( 2 ) = 2 , obwohl es sich hierbei um eine Figur im dreidimensionalen Raum handelt. Mit einer zunehmenden Zahl von Iterationsschritten geht das Volumen der Figur gegen 0, der Flächeninhalt der Oberfläche bleibt jedoch konstant, weil sich die Anzahl der Seitenflächen der zueinander deckungsgleichen Teil-Tetraeder mit jedem Iterationsschritt vervierfacht, während sich die Seitenlänge dieser Seitenflächen, die alle deckungsgleiche Dreiecke sind, halbiert.
Interessant ist, dass sich das im Fall eines regelmäßigen Sierpinski-Tetraeders auch wie folgt einsehen lässt:

Die doppelte und quadratische Projektionsfläche hilft zu zeigen, dass die Oberfläche nach jedem Iterationsschritt konstant bleibt.
Werden alle Seitenflächen des regelmäßigen Sierpinski-Tetraeders, also gleichseitige Dreiecke, mit einer Parallelprojektion auf eine Ebene, die parallel zu zwei seiner gegenüber liegenden und zueinander orthogonalen Kanten ist, projiziert, dann entsteht als projizierte Fläche ein Quadrat, wobei auf jede Teilfläche des Quadrats jeweils zwei Seitenflächen des Sierpinski-Tetraeders projiziert werden (siehe Animation). Die Projektionsflächen der vier gleichseitigen Dreiecke der ebenfalls regelmäßigen Teil-Tetraeder sind jeweils zueinander parallele und gleich große Teilquadrate des gesamten Quadrates, die eine quadratische und platonische Parkettierung bilden. Jedes einzelne gleichseitige Dreieck bildet bei der Projektion ein gleichschenkliges und rechtwinkliges Dreieck mit den Innenwinkeln 45°, 45° und 90°. Die vier Seitenflächen eines Teil-Tetraeders erzeugen dann jeweils ein doppelt projiziertes Teilquadrat.
Mit jedem Iterationsschritt vervierfacht sich die Anzahl der Teil-Tetraeder, also vervierfacht sich auch die Anzahl der doppelt projizierten Teilquadrate, aber die Seitenlänge der Teilquadrate halbiert sich, sodass der Flächeninhalt der doppelten und quadratischen Projektionsfläche konstant bleibt. Weil alle Seitenflächen des regelmäßigen Sierpinski-Tetraeders mit der Projektionsebene denselben Diederwinkel bilden, ist jede einzelne projizierte Teilfläche um denselben Faktor kleiner als die ursprüngliche Seitenfläche.
Daraus folgt dann: Wenn der Flächeninhalt der doppelten und quadratischen Projektionsfläche nach jedem Iterationsschritt konstant bleibt, muss auch der Flächeninhalt der gesamten Oberfläche des regelmäßigen Sierpinski-Tetraeders konstant bleiben. Diese Betrachtungen lassen sich mithilfe einer affinen Abbildung auch auf ein beliebiges Sierpinski-Tetraeder verallgemeinern.
Verallgemeinerung auf n Dimensionen
Der zweidimensionale Fall des Sierpinski-Dreiecks lässt sich auf n Dimensionen verallgemeinern. Die Startfigur ist dann ein Simplex. In diesem n -dimensionalen Sierpinski-Simplex sind die übriggebliebenen geometrischen Figuren n -dimensionale Teil-Simplexe und die herausgeschnittenen geometrischen Figuren sind rektifizierte n -dimensionale Simplexe (siehe Archimedischer Körper – Ableitungen aus den platonischen Körpern).
Die unter Mathematische Zusammenhänge dargestellten Betrachtungen für lassen sich problemlos auf n Dimensionen und damit auf die n -dimensionale Volumens der Teil-Simplexe dieses n -dimensionalen Sierpinski-Simplexes und deren n − 1 -dimensionale Oberflächen der verallgemeinern. Die Anordnung dieser Teil-Simplexe und deren Oberflächen zueinander ist etwas komplizierter.
Zusammenhang mit regelmäßigen dreidimensionalen Parkettierungen

Das regelmäßige Sierpinski-Tetraeder steht im Zusammenhang mit der regelmäßigen dreidimensionalen Parkettierung (siehe Raumfüllung), die aus kongruenten regelmäßigen Tetraedern und Oktaedern besteht, und den dreidimensionalen euklidischen Raum vollständig ausfüllt. Dabei treffen in jeder Ecke jeweils 8 Oktaeder und 6 Tetraeder zusammen (siehe Abbildung), die den vollen Raumwinkel von 4 ⋅ π s r ≈ 12,566 s r ausfüllen. Diese Parkettierung bildet Schichten, die jeweils von zwei parallelen Ebenen im Raum begrenzt werden. Jedes Oktaeder bildet zusammen mit 2 Tetraedern, die an zwei gegenüberliegenden Seitenflächen des Oktaeders liegen ein Rhomboeder. Diese Rhomboeder haben als Seitenflächen 6 Rauten, die aus jeweils 2 gleichseitigen Dreiecken gebildet werden, also die Innenwinkel 60°, 120°, 60°, 120° haben. Diese Rhomboeder bilden ein Gitter aus parallelen Ebenen, die durch die Parkettierung verlaufen und die einzelnen Polyeder an den Seitenflächen berühren, aber nicht schneiden.
Diese regelmäßige Parkettierung ist spiegelsymmetrisch, punktsymmetrisch, drehsymmetrisch und translationssymmetrisch und neben dem Kubusgitter die einzige, die den dreidimensionalen Raum vollständig mit platonischen Körpern gleicher Seitenlänge ausfüllt.
Die gezeigte regelmäßige dreidimensionale Parkettierung ist eine feinere Zerlegung des regelmäßigen Sierpinski-Tetraeders nach dem Iterationsschritt k .
Dabei werden die herausgeschnittenen Oktaeder des Iterationschritts i , deren Kantenlänge um den Faktor 2 k − i größer als die Kantenlänge der übriggebliebenen regelmäßigen Tetraeder ist, jeweils in 8 ⋅ ( 2 k − i + 1 3 ) = 2 k − i ⋅ ( 8 ⋅ 4 k − i − 8 ) 6 kongruente Tetraeder und ( 2 k − i + 2 3 ) + 2 ⋅ ( 2 k − i + 1 3 ) + ( 2 k − i 3 ) = 2 k − i ⋅ ( 4 ⋅ 4 k − i + 2 ) 6 kongruente Oktaeder mit dieser Kantenlänge zerlegt. Das äußere Gebiet, das theoretisch ins Unendliche des dreidimensionalen Raums geht, wird ebenfalls in Tetraeder und Oktaeder und zerlegt. Das regelmäßige Sierpinski-Dreieck nach dem Iterationsschritt k überdeckt ( 2 k + 2 3 ) + ( 2 k 3 ) = 2 k ⋅ ( 2 ⋅ 4 k + 4 ) 6 Tetraeder und ( 2 k + 1 3 ) = 2 k ⋅ ( 4 k − 1 ) 6 Oktaeder der regelmäßigen dreidimensionalen Parkettierung.
Dabei gibt es zwei verschiedene disjunkte Mengen von Tetraedern. Die Seitenflächen und Kanten der Tetraeder beider Mengen liegen jeweils parallel zueinander, aber ihre Ecken zeigen bezogen auf die gegenüberliegende Seitenfläche jeweils in entgegengesetzte Richtungen. Sowohl die Tetraeder als auch die Oktaeder sind in einer Tetraeder-förmigen Formation angeordnet. Die Anzahlen der Polyeder der dreidimensionale Parkettierung, die vom regelmäßige Sierpinski-Tetraeder überdeckt werden, sind daher Tetraederzahlen, die Binomialkoeffizienten im Pascalschen Dreieck sind.
Die kongruenten Tetraeder und Oktaeder müssen nicht regelmäßig sein. Mithilfe einer affinen Abbildung kann das Sierpinski-Tetraeder zusammen mit der dreidimensionalen Parkettierung (Raumfüllung) auf beliebige Tetraeder verallgemeinert werden.
Weitere Verallgemeinerungen

Das ursprüngliche Dreieck (Ausgangsdreieck) und die Teildreiecke können mit jedem Iterationsschritt statt in 2 2 = 4 auch allgemein in m 2 deckungsgleiche Dreiecke zerlegt werden. Die Berechnungen können für diese Fälle ohne Ausnahme verallgemeinert werden.[4][5]
Das gelöschte Dreieck bei jedem Iterationsschritt muss nicht ähnlich zum Ausgangsdreieck sein. Dann liegen die Ecken nicht unbedingt äquidistant auf den Seiten des Teildreiecks und die Seiten sind nicht unbedingt parallel. Daraus ergeben sich weitere Verallgemeinerungen. Die geometrischen Berechnungen werden dann komplizierter.[6]
Eine weitere Verallgemeinerung ergibt sich, wenn als Ausgangsfigur nicht ein Dreieck, sondern ein regelmäßiges Polygon oder sogar ein beliebiges konvexes Polygon gewählt und mit jedem Iterationsschritt die Mittelpunkte der Seiten der bisherigen Teil-Polygone verbunden werden. Dann würden die dadurch neu entstandenen Polygone gelöscht und dieses Verfahren mit jedem Iterationsschritt k wiederholt. Die dadurch entstehenden Seitenverhältnisse wären komplizierter und würden entscheidend von der Ausgangsfigur, also dem regelmäßigen oder konvexen Polygon, abhängen. Innerhalb der entstandenen Teildreiecke ergibt sich immer eine äquidistante Aufteilung wie beim Sierpinski-Dreieck, wo die Seitenverhältnisse von den Seitenverhältnissen des ursprüngliche Dreiecks und von den Zweierpotenzen 2 k abhängen.
Graphentheoretische Eigenschaften
Vollständig gefüllter Baum
Graphentheoretisch können die gelöschten Dreiecke des Sierpinski-Dreiecks nach dem Iterationsschritt k einem vollständig gefüllten Baum mit k + 1 „Zeilen“ bijektiv zugeordnet werden, wobei der Knotengrad der „Wurzel“ des Baums gleich 3, der Knotengrad der inneren Knoten gleich 4 und der Knotengrad der „Blätter“ wie bei jedem Baum gleich 1 ist. Das ist ein sogenannter vollständiger ternärer Baum, eine Verallgemeinerung eines vollständigen Binärbaums.
Im dreidimensionalen Fall, also dem Sierpinski-Tetraeder, ist der Knotengrad der „Wurzel“ gleich 4 und der Knotengrad der inneren Knoten gleich 5. Dabei werden in diesem Fall die Knoten den gelöschten Tetraedern bijektiv zugeordnet.
Entsprechend ist dieser Knotengrad im n -dimensionalen Fall, also dem n –dimensionalen Sierpinski-Simplex, gleich n + 1 (siehe Weitere Verallgemeinerungen).
Sierpinski-Graph
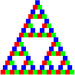
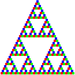
Der Sierpinski-Graph ist eine Darstellung des Sierpinski-Dreiecks als ungerichteter Graph. Jede Ecke der Teildreiecke stellt dabei einen Knoten, jede Seite eines Teildreiecks eine Kante und jedes Teildreieck eine Fläche des Graphen dar. Dieser Graph ist offensichtlich zusammenhängend. Der Sierpinski-Graph für den Iterationsschritt k besteht aus E = 3 2 ⋅ ( 3 k + 1 ) Knoten, K = 3 k + 1 Kanten und F = 1 2 ⋅ ( 3 k + 1 + 1 ) Flächen, wenn die äußere Fläche mitgezählt wird. Weil er ein planarer Graph ist, gilt nach dem Eulerschen Polyedersatz E − K + F = 2 .
Fast alle Knoten haben den Grad 4. Nur die 3 Knoten, die den Ecken des Ausgangsdreiecks zugeordnet sind, haben den Grad 2. Weil alle Knotengrade gerade sind, besitzt dieser Graph Eulerkreise. Er enthält auch Hamiltonkreise, wie sich mithilfe von vollständiger Induktion zeigen lässt.[7]
Die chromatische Zahl des Sierpinski-Graphen ist 3, weil sich die Knoten das Dreiecksgitters mit 3 verschiedenen Farben eingefärbt werden kann (siehe Knotenfärbung) und der Graph ein Teilgraph dieses Dreiecksgitters ist. Der Sierpinski-Graph hat außerdem den chromatischen Index 4 (siehe Kantenfärbung). Seine Flächen können per Definition mit 2 verschiedenen Farben eingefärbt werden, sodass es keine benachbarten Flächen mit gleicher Farbe gibt.[8]
Chaos-Spiel

Abgesehen von der rekursiven Darstellung gibt es noch einen Zufallspunkt–Algorithmus zur näherungsweisen Konstruktion des Sierpinski-Dreiecks: Das „Chaos-Spiel“.
Dabei wird ein gleichseitiges Dreieck mit den Ecken A, B, C aufgezeichnet und ein zufälliger Punkt im Inneren des Dreiecks gewählt. Er kann aber auch außerhalb liegen, ohne das Ergebnis wesentlich zu verändern. Nun wird pro Schritt eine Ecke zufällig ausgewählt und der Punkt gedanklich mit der gezogenen Ecke verbunden. Die Wahrscheinlichkeiten für die Ecken sind jeweils gleich. Die Mitte dieser Strecke markiert nun den Punkt für die nächste Runde. Wiederholt man dies sehr oft, bilden die Punkte eine Näherung des Sierpinski-Dreiecks. Wenn man die Punkte auch noch je nach ausgewählter Ecke unterschiedlich einfärbt, also z. B. A = grün, B = rot und C = blau, dann bekommt man drei unterschiedlich gefärbte Sierpinski-Dreiecke im Sierpinski-Dreieck.
Man kann aus der iterativen Struktur des Sierpinski-Dreiecks beweisen, dass ein mittels dieses Zufallszahlen-Algorithmus gewonnener Punkt genau dann zum Sierpinski-Dreieck gehört, wenn auch der Ausgangspunkt Teil des Sierpinski-Dreiecks ist. Wenn man also beispielsweise einen Punkt der Strecke AB als Ausgangspunkt wählt, hat man nach unendlich vielen Iterationen ein Sierpinski-Dreieck konstruiert.
Zusammenhang mit dem Pascalschen Dreieck

Mit dem Sierpinski-Dreieck verwandt ist das Pascalsche Dreieck. Dabei entsprechen die geraden Zahlen im Pascal-Dreieck, die Binomialkoeffizienten, den gelöschten Teildreiecken im Sierpinski-Dreieck und die ungeraden Zahlen den übriggebliebenen Teildreiecken. Beide Dreiecke haben eine einfache Iterationsvorschrift, aus der stets eine geometrische Ähnlichkeit hervorgeht: Wird in einem Schritt beim Sierpinski-Dreieck jedes Initiatordreieck nach oben bereits beschriebener Regel ersetzt, so wird beim Pascal-Dreieck lediglich die Anzahl der Zeilen verdoppelt. Ungerade Zahlen mit mehr als einer Dezimalstelle werden im Folgenden der übersichtlicheren Darstellung halber als # dargestellt.
Initiator:
1
1 1
1. Schritt
1
1 1
1 1
1 3 3 1
2. Schritt
1
1 1
1 1
1 3 3 1
1 1
1 5 5 1
1 # # 1
1 7 # # # # 7 1
Diese Ähnlichkeit ist sowohl für ein unendliches Pascal-Dreieck als auch ein Sierpinski-Dreieck nach unendlich vielen Iterationsschritten gegeben.
Das Erzeugen dieser Ähnlichkeit kann auch aus einer anderen Sichtweise betrachten werden: Das Pascal-Dreieck selbst ist als Idee und damit als geometrischer Bauplan immer unendlich, wir können es nur nicht komplett aufschreiben. Ein iterativ erzeugtes Sierpinski-Dreieck aber ist stets durch seine konvexe Hülle beschränkt. Somit wird durch fortlaufende Iteration nicht das Pascal-Dreieck an ein Sierpinski-Dreieck, sondern das Sierpinski-Dreieck an den unendlichen geometrischen Bauplan und damit an das unendliche Pascal-Dreieck angeglichen.
Der Zusammenhang zwischen den geraden oder ungeraden Zahlen (Binomialkoeffizienten) und den Teildreiecken lässt sich formal so aufschreiben:
- Jedes übriggebliebene Teildreieck des Sierpinski-Dreiecks ist genau einem ungeraden Binomialkoeffizient des partiellen Pascal-Dreiecks mit 2 k Zeilen zugeordnet und umgekehrt, nämlich dann, wenn ( a b ) m o d 2 = a ! b ! ⋅ ( a − b ) ! m o d 2 = 1 ist. Diese Zuordnung ist also bijektiv.
- Jedes gelöschte Teildreieck des Sierpinski-Dreiecks ist – mit Ausnahme der letzten Iteration – genau einem geraden Binomialkoeffizient des partiellen Pascal-Dreiecks mit 2 k Zeilen zugeordnet und umgekehrt, nämlich dann, wenn ( a b ) m o d 2 = a ! b ! ⋅ ( a − b ) ! m o d 2 = 0 ist. Diese Zuordnung ist also injektiv und nicht bijektiv.
Für einen effizienten iterativen Algorithmus, der die binären Ziffern 0 und 1 für die geraden oder ungeraden Zahlen des Pascal-Dreiecks berechnet, ist es nicht sinnvoll, die Binomialkoeffizienten zu berechnen, sondern zeilenweise eine simple binäre Addition modulo 2 auszuführen (siehe Binomialkoeffizient – Divisionsreste).[9]
Für das verallgemeinerte Sierpinski-Dreieck, wo mit jedem Iterationsschritt die übriggebliebenen Teildreiecke statt in 2 2 = 4 , jeweils in m 2 deckungsgleiche Dreiecke zerlegt werden (siehe Weitere Verallgemeinerungen), werden die übriggebliebenen Teildreiecke einem Binomialkoeffizienten zugeordnet, wenn dieser nicht durch m teilbar ist, also ( a b ) m o d m = a ! b ! ⋅ ( a − b ) ! m o d m > 0 gilt. Für die durch m teilbaren Zahlen ist die Zuordnung zu den gelöschten Teildreiecken entsprechend wie für den genannten Standardfall m = 2.
Dabei ist zu beachten, dass am rechten und am linken Rand des Pascal-Dreiecks in der Zeile m k , wobei m der Zerlegungsfaktor für die übriggebliebenen Teildreiecke und k die Anzahl der Iterationsschritte ist, der Binomialkoeffizient gleich 1 ist, und alle anderen Zahlen, die dazwischen stehen, gleich 0. Deshalb fängt das Pascal-Dreieck modulo m für jeden Iterationsschritt k mit der Zeile m k sozusagen von vorn an. Formal lässt sich das als ( m k 0 ) m o d m = ( m k m k ) m o d m = 1 und ( m k b ) m o d m = 0 für 0 < b < m k ausdrücken.[10]
Für einen effizienten iterativen Algorithmus ist es auch in diesem allgemeineren Fall sinnvoller, simple Additionen modulo m auszuführen.
Solche Betrachtungen spielen in der Informatik für die Laufzeiten und die Komplexitätstheorie eine Rolle.
Programmierung
Das Sierpinski-Dreieck lässt sich sowohl rekursiv als auch iterativ implementieren. Der Code der rekursiven Programmierung ist kürzer, weil die Koordinaten der Punkte nicht in einer Liste oder einem Array gespeichert werden müssen. Die folgenden Beispiele zeigen eine rekursive und eine iterative Implementierung in der Programmiersprache C#.
Rekursive Implementierung
using System.Windows.Forms;
public class MainForm : System.Windows.Forms.Form
{
private Graphics graphics;
public MainForm()
{
InitializeComponent();
Text = "Sierpinski-Dreieck";
Width = 800;
Height = 600;
graphics = CreateGraphics(); // Erzeugt ein Grafikobjekt für das Zeichnen auf dem Hauptfenster.
Paint += OnPaint; // Verknüpft die Ereignisbehandlungsmethode mit dem Paint Ereignis des Hauptfensters.
}
private void OnPaint(object sender, PaintEventArgs e)
{
ZeichneSierpinskiDreieck(200, 400, 600, 400, Color.FromArgb(0, 0, 0), 0, 4); // Aufruf der Methode mit maximaler Rekursionstiefe 4
}
// Diese Methode wird aufgerufen, wenn das Hauptfenster gezeichnet wird. Sie enthält 3 rekursive Aufrufe.
private void ZeichneSierpinskiDreieck(float x1, float y1, float x2, float y2, Color farbe, int tiefe, int maximaleTiefe)
{
float faktor = (float) Math.Sqrt(3) / 2; // Skalierungsfaktor für die Höhe der gleichseitigen Dreiecke
if (tiefe == maximaleTiefe) // Wenn maximale Rekursionstiefe erreicht, dann Koordinaten setzen und gleichseitiges Dreieck ausfüllen
{
PointF[] dreieck = new PointF[]{new PointF(x1, y1), new PointF(x2, y2), new PointF((float) ((x1 + x2) / 2 + faktor * (y2 - y1)), (float) ((y1 + y2) / 2 + faktor * (x1 - x2)))};
graphics.FillPolygon(new SolidBrush(farbe), dreieck); // Füllt das gleichseitige Dreieck mit den gesetzten Koordinaten der als Parameter angegebenen Farbe aus.
}
else // sonst Methode für jeden der 3 Teilbereiche rekursiv aufrufen
{
// Definiert Farben mit RGB-Werten.
Color rot = Color.FromArgb(255, 0, 0), grün = Color.FromArgb(0, 255, 0), blau = Color.FromArgb(0, 0, 255);
// Rekursive Aufrufe der Methode für das Zerlegen des aktuellen Dreiecks in 3 Teilbereiche mit halber Breite und Höhe.
ZeichneSierpinskiDreieck(x1, y1, (x1 + x2) / 2, (y1 + y2) / 2, rot, tiefe + 1, maximaleTiefe);
ZeichneSierpinskiDreieck((x1 + x2) / 2, (y1 + y2) / 2, x2, y2, grün, tiefe + 1, maximaleTiefe);
ZeichneSierpinskiDreieck((float) ((3 * x1 + x2) / 4 + faktor * (y2 - y1) / 2), (float) ((3 * y1 + y2) / 4 + faktor * (x1 - x2) / 2), (float) ((x1 + 3 * x2) / 4 + faktor * (y2 - y1) / 2), (float) ((y1 + 3 * y2) / 4 + faktor * (x1 - x2) / 2), blau, tiefe + 1, maximaleTiefe);
}
}
}
Iterative Programmierung
Hier werden nur die Methode für die Berechnung der Koordinaten und das Zeichnen der einzelnen Dreiecke gezeigt.
private void BerechneKoordinaten(ref List<float> x1Werte, ref List<float> y1Werte, ref List<float> x2Werte, ref List<float> y2Werte, ref List<Color> farben)
{
double faktor = Math.Sqrt(3) / 2; // Skalierungsfaktor für die Höhe der gleichseitigen Dreiecke
List<float> neueX1Werte = new List<float>(), neueY1Werte = new List<float>(), neueX2Werte = new List<float>(), neueY2Werte = new List<float>();
List<Color> neueFarben = new List<Color>();
int anzahlDerTeilDreiecke = farben.Count;
for (int i = 0; i < anzahlDerTeilDreiecke; i++)
{
float x1 = x1Werte[i], y1 = y1Werte[i], x2 = x2Werte[i], y2Werte[i];
neueX1Werte.Add(x1);
neueY1Werte.Add(y1);
neueX2Werte.Add((x1 + x2) / 2);
neueY2Werte.Add((y1 + y2) / 2);
neueX1Werte.Add((x1 + x2) / 2);
neueY1Werte.Add((y1 + y2) / 2);
neueX2Werte.Add(x2);
neueY2Werte.Add(y2);
neueX1Werte.Add((float) ((3 * x1 + x2) / 4 + faktor * (y2 - y1) / 2));
neueY1Werte.Add((float) ((3 * y1 + y2) / 4 + faktor * (x1 - x2) / 2));
neueX2Werte.Add((float) ((x1 + 3 * x2) / 4 + faktor * (y2 - y1) / 2));
neueY2Werte.Add((float) ((y1 + 3 * y2) / 4 + faktor * (x1 - x2) / 2));
}
x1Werte = neueX1Werte;
y1Werte = neueY1Werte;
x2Werte = neueX2Werte;
y2Werte = neueY2Werte;
}
private void ZeichneDreieck(float x1, float y1, float x2, float y2, Color farbe)
{
double faktor = Math.Sqrt(3) / 2; // Skalierungsfaktor für die Höhe der gleichseitigen Dreiecke
PointF[] dreieck = new PointF[]{new PointF(x1, y1), new PointF(x2, y2), new PointF((float) ((x1 + x2) / 2 + faktor * (y2 - y1)), (float) ((y1 + y2) / 2 + faktor * (x1 - x2)))};
graphics.FillPolygon(new SolidBrush(farbe), dreieck); // Füllt das gleichseitige Dreieck mit der als Parameter angegebenen Farbe aus.
}
Natur
In der Natur kommt dieses Muster auf dem Gehäuse der Schneckenart Cymbiola innexa vor.[11][12]
Siehe auch
- Sierpinski-Kurve
- Sierpinski-Teppich
- Fraktalantenne
- Türme von Hanoi
- Tetraeder (Bottrop)
- Triforce
- Grand Egyptian Museum
Literatur
- P. S. Alexandroff: Einführung in die Mengenlehre und in die allgemeine Topologie (= Hochschulbücher für Mathematik. Band 85). VEB Deutscher Verlag der Wissenschaften, Berlin 1984.
Weblinks
- Eric W. Weisstein: Sierpiński Sieve. In: MathWorld (englisch).
- Erklärungen zu Chaosspiel und Sierpinsky-Dreieck
- Interaktive Konstruktion zum Ausprobieren mit JSXGraph
- Erklärung und Java-Applet zum Chaos-Spiel
- Fraktale – Wechselspiel zwischen Chaos und Ordnung, Universität Berlin
- Demonstration des Sierpinski-Dreiecks mit WolframAlpha
- Sierpinski sieve generator, onlinemathtools.com
- Sierpinski arrowhead curve generator, onlinemathtools.com
- Implementierung in .NET


 Iterationsschritten für k ≤ 4
Iterationsschritten für k ≤ 4  :
:


 Teildreicke gleicher Seitenlänge übrig und es werden 3 k − 1 2
Teildreicke gleicher Seitenlänge übrig und es werden 3 k − 1 2 
 hat, beträgt sein
hat, beträgt sein  .
. entfernt. Mit jedem Schritt verdreifacht sich die Anzahl der Dreiecke und die Seitenlänge halbiert sich, sodass beim Iterationsschritt k
entfernt. Mit jedem Schritt verdreifacht sich die Anzahl der Dreiecke und die Seitenlänge halbiert sich, sodass beim Iterationsschritt k  Dreiecke mit der Seitenlänge a 2 k
Dreiecke mit der Seitenlänge a 2 k  entfernt werden. Der Flächeninhalt der gelöschten Dreiecke beim Iterationsschritt k
entfernt werden. Der Flächeninhalt der gelöschten Dreiecke beim Iterationsschritt k  . Der gesamte Flächeninhalt der gelöschten Dreiecke nach dem Iterationsschritt k
. Der gesamte Flächeninhalt der gelöschten Dreiecke nach dem Iterationsschritt k  und der Flächeninhalt der übriggebliebenen Teildreicke ist gleich A k = ( 3 4 ) k ⋅ 3 4 ⋅ a 2
und der Flächeninhalt der übriggebliebenen Teildreicke ist gleich A k = ( 3 4 ) k ⋅ 3 4 ⋅ a 2  . Dabei wurde eine so genannte
. Dabei wurde eine so genannte  berechnet.
berechnet. , oder anders ausgedrückt, er
, oder anders ausgedrückt, er  . Nach k
. Nach k  ausdrücken. Entscheidend ist dabei, dass die Seitenlänge a
ausdrücken. Entscheidend ist dabei, dass die Seitenlänge a  . Dies resultiert daraus, dass sich die Anzahl der Teildreiecke mit jedem Schritt verdreifacht, also beim Schritt k
. Dies resultiert daraus, dass sich die Anzahl der Teildreiecke mit jedem Schritt verdreifacht, also beim Schritt k  , deren Seitenlänge um den Faktor 2 k − i
, deren Seitenlänge um den Faktor 2 k − i  größer als die Seitenlänge der übriggebliebenen
größer als die Seitenlänge der übriggebliebenen  kongruente gleichseitige Dreiecke mit dieser Seitenlänge zerlegt. Das äußere Gebiet, das theoretisch ins
kongruente gleichseitige Dreiecke mit dieser Seitenlänge zerlegt. Das äußere Gebiet, das theoretisch ins  Dreiecke des regelmäßigen Dreiecksgitters.
Dreiecke des regelmäßigen Dreiecksgitters.

 . Es stellt ein im R 2
. Es stellt ein im R 2  .
. , obwohl es sich hierbei um eine Figur im dreidimensionalen Raum handelt. Mit einer zunehmenden Zahl von Iterationsschritten geht das
, obwohl es sich hierbei um eine Figur im dreidimensionalen Raum handelt. Mit einer zunehmenden Zahl von Iterationsschritten geht das 
 -dimensionale Oberflächen der verallgemeinern. Die Anordnung dieser Teil-Simplexe und deren Oberflächen zueinander ist etwas komplizierter.
-dimensionale Oberflächen der verallgemeinern. Die Anordnung dieser Teil-Simplexe und deren Oberflächen zueinander ist etwas komplizierter. ausfüllen. Diese Parkettierung bildet Schichten, die jeweils von zwei parallelen Ebenen im Raum begrenzt werden. Jedes Oktaeder bildet zusammen mit 2 Tetraedern, die an zwei gegenüberliegenden Seitenflächen des Oktaeders liegen ein
ausfüllen. Diese Parkettierung bildet Schichten, die jeweils von zwei parallelen Ebenen im Raum begrenzt werden. Jedes Oktaeder bildet zusammen mit 2 Tetraedern, die an zwei gegenüberliegenden Seitenflächen des Oktaeders liegen ein 
 kongruente Oktaeder mit dieser Kantenlänge zerlegt. Das äußere Gebiet, das theoretisch ins
kongruente Oktaeder mit dieser Kantenlänge zerlegt. Das äußere Gebiet, das theoretisch ins 
 Oktaeder der regelmäßigen dreidimensionalen Parkettierung.
Oktaeder der regelmäßigen dreidimensionalen Parkettierung. auch allgemein in m 2
auch allgemein in m 2 
 abhängen.
abhängen. „Zeilen“
„Zeilen“  (siehe
(siehe  Knoten, K = 3 k + 1
Knoten, K = 3 k + 1  Kanten und F = 1 2 ⋅ ( 3 k + 1 + 1 )
Kanten und F = 1 2 ⋅ ( 3 k + 1 + 1 )  Flächen, wenn die äußere Fläche mitgezählt wird. Weil er ein
Flächen, wenn die äußere Fläche mitgezählt wird. Weil er ein  .
. ist. Diese Zuordnung ist also
ist. Diese Zuordnung ist also  ist. Diese Zuordnung ist also
ist. Diese Zuordnung ist also  teilbar ist, also ( a b ) m o d m = a ! b ! ⋅ ( a − b ) ! m o d m > 0
teilbar ist, also ( a b ) m o d m = a ! b ! ⋅ ( a − b ) ! m o d m > 0  gilt. Für die durch m
gilt. Für die durch m 
 , wobei m
, wobei m  und ( m k b ) m o d m = 0
und ( m k b ) m o d m = 0  für 0 < b < m k
für 0 < b < m k  ausdrücken.
ausdrücken.